|
|
|
|






Every finitely realizable physical system can be
perfectly simulated by a universal model computing machine operating by finite
means. _ |
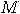 is capable
of perfectly simulating a physical system
is capable
of perfectly simulating a physical system 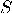 , under given labelling of inputs and outputs, if there is a
program for
, under given labelling of inputs and outputs, if there is a
program for 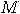 that makes
that makes 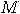 computationally equivalent to
computationally equivalent to 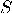 under that labelling. Re-phrased,
under that labelling. Re-phrased, 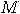 becomes under a certain program and a fixed
labelling, a system “computationally indistinguishable" from
becomes under a certain program and a fixed
labelling, a system “computationally indistinguishable" from 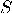 . Deutsch [48], p.100, argued that the above principle
is stronger than the Church–Turing Thesis: it is not satisfied by Turing machines in classical physics,
but it is compatible with quantum theory. This observation motivates the interest, and the urgency, in
seeking a “truly quantum" model of computation.
. Deutsch [48], p.100, argued that the above principle
is stronger than the Church–Turing Thesis: it is not satisfied by Turing machines in classical physics,
but it is compatible with quantum theory. This observation motivates the interest, and the urgency, in
seeking a “truly quantum" model of computation. 
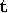 , and a control consisting of a
finite sequence of qubits,
, and a control consisting of a
finite sequence of qubits, 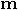 . In addition,
Deutsch uses an observable,
. In addition,
Deutsch uses an observable, 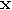 , which has
an integer as possible value. The state of the quantum computer is a unit
vector in the space spanned by basis vectors
, which has
an integer as possible value. The state of the quantum computer is a unit
vector in the space spanned by basis vectors 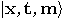 . The dynamics is given by a constant unitary
operator
. The dynamics is given by a constant unitary
operator 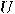 . With these ingredients, Deutsch
[48] has described a universal quantum
computer, that is one capable of simulating perfectly every finitely realizable
physical system (hence, every quantum computer). As applications he proposed
the random generation procedure described in Section 3.6.
. With these ingredients, Deutsch
[48] has described a universal quantum
computer, that is one capable of simulating perfectly every finitely realizable
physical system (hence, every quantum computer). As applications he proposed
the random generation procedure described in Section 3.6. 

