|
|
|
|
| in a strict sense quantum theory is a set of rules
allowing the computation of probabilities for the outcomes of tests which
follow specific preparations. |
| physical reality is irreducible random. |
) generating a binary string is the program-size complexity of the string. This idea can be extended in an appropriate
way to infinite sequences. A random string/sequence is incompressible as
the smallest program for generating it is the string/sequence itself! Strings/sequences
that can be generated by small programs are deemed to be less random than
those requiring longer programs. For example, the digits of 
can be computed one by one;
nonetheless, if examined locally, without being aware of their provenance,
they appear “random". People have calculated 
out to a billion or more digits. A reason for doing this is
the question of whether each digit occurs the same number of times, a sympton
of randomness. It seems, but remains unproven, that the digits 0 through
9 each occur 10% of the time in a decimal expansion of . If this turns out to be true, then would be a so-called simply normal real number.
But although may be random in so far as
it’s “normal", it is far from (algorithmic) random, because its infinity
of digits can be compressed into a concise program for calculating them.
The numbers generated by the so-called logistic map,  |
(9) |
is an arbitrary constant and the process starts at some state
, may appear “random" for
some values, say 
and 
; however, they are not, because of the succinctness
of the rule (9) describing them. In Figure
3.6 we will show the evolution of
130 iterates of the logistic map, all starting from , with 
.
| Anyone who considers arithmetical methods of producing
random digits is, of course, in a state of sin. |
over the alphabet
and define a new sequence
, over the alphabet 
, by 
and 
(and,
infinitely many more others) never appear, so the sequence has clear regularities
(which can, actually, be detected by simple statistical randomness tests).
is a random binary string,
then break the string into pairs and then code 
, 
, 
, 
by 
: the result is again a random
sequence. So, the problem is to start from an initial state which can be
precisely controlled and has a low program-size complexity and produce measurements
of unbounded program-size complexity out its natural dynamical evolution.
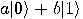through
an angle 
. In particular, 
transforms that state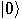 
into an equally weighted superposition
of 0 and 1:  |
(10) |
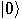state, apply the operator to rotate the state into the
superposition (10), and the observe the superposition.
The act of observation produces the collapse into eithe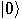r or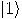 
, with equal chances. Consequently, one can use
the quantum superposition and indeterminism to simulate, with probability
one, a “fair" coin toss. Random digits produced with quantum random generators
of the type described above are, with probability one, free of subtle correations
that haunt classical pseudo-random number generators. Of course, the problem
of producing algorithmic random strings is still open. Indeed,
let us assume that we have a classical silicon computer that simulates, using
a high-quality pseudo-random generator, the quantum mechanics dynamics and
quantum measurement of a 2-state quantum system. The simulated world will
be statistically almost identical (up to some degree) with the “real" quantum
system. However, all simulated bits will be, in the long run, highly compressible.
How can we be sure that the “real" quantum system is not just a superpowerful
pseudo-random generator? 
For technical
reasons, we use self-delimiting Turing machines, machines having a “prefix-free"
domain: no proper extension of a program that eventually halts has that property.
