|
|
|
|

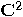 .
. 

the transformation 
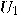 and and 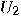 are unitary transformations acting on are unitary transformations acting on 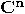 , is also unitary. , is also unitary.  |

 |
The controlled-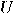 gate _ gate _
 is the single-qubit identity and is the single-qubit identity and
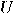 is another single-qubit gate which
can be used in the particular case of is another single-qubit gate which
can be used in the particular case of 
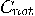 . .  |
 |
The gate 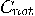 cannot be used to “copy"
a qubit in an unknown state. Indeed, if we assume that the qubit was in the
state cannot be used to “copy"
a qubit in an unknown state. Indeed, if we assume that the qubit was in the
state 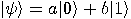 . We use as input . We use as input
 and and 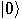 , that is, , that is, 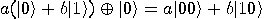 , and we apply , and we apply  to it. The result is to it. The result is 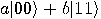 . The two qubits are apparently
in the same state, so we have contradicted the no cloning theorem! . The two qubits are apparently
in the same state, so we have contradicted the no cloning theorem!  The explanation is simple. When we measure one of the qubits we get 0 or 1 with probabilities 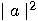 and and
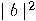 . But, once we measure
one qubit, the state of the other qubit is completely determined, so no extra
information can be obtained about . But, once we measure
one qubit, the state of the other qubit is completely determined, so no extra
information can be obtained about  , so the hidden information carried by , so the hidden information carried by  is lost because it was not
copied. Although the two qubits appear to be identical, they are not independent
copies from is lost because it was not
copied. Although the two qubits appear to be identical, they are not independent
copies from  : they are two
entangled qubits carrying together only one qubit of information. : they are two
entangled qubits carrying together only one qubit of information.  |
 |
The controlled-controlled-NOT
(Toffoli) gate can be obtained from (12
) by taking 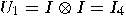 and and 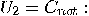 

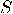 is the swap operation is the swap operation 
 |

The transformation  given by (12) is universal
for all Boolean circuits. given by (12) is universal
for all Boolean circuits.  |
 given by (12). We have
given by (12). We have 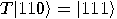 and
and 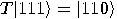 , hence the third bit is changed, that is
, hence the third bit is changed, that is 
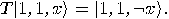
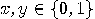 ,
, 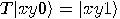 if and only if
if and only if 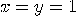 , and
, and 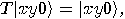 otherwise.
Consequently, the last bit of
otherwise.
Consequently, the last bit of 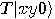 is
is 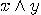 ,
, 
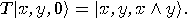
 or
or 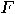 quantum gates are universal for Boolean circuits,
they cannot achieve any quantum state transformation. Universality
for quantum transformation is defined differently as we are dealing with
continuous, not discrete, transformations, and the maximum one can hope for
is an arbitrarily good approximation. A matrix
quantum gates are universal for Boolean circuits,
they cannot achieve any quantum state transformation. Universality
for quantum transformation is defined differently as we are dealing with
continuous, not discrete, transformations, and the maximum one can hope for
is an arbitrarily good approximation. A matrix 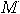 is
is  -close to a unitary matrix
-close to a unitary matrix
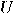 if
if 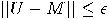 . ()Recall that
. ()Recall that 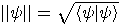 is the norm.) A set of quantum gates
is the norm.) A set of quantum gates 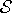 is universal
for quantum transformations if every
unitary transformation
is universal
for quantum transformations if every
unitary transformation 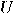 can be performed
with arbitrary precision
can be performed
with arbitrary precision 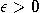 by a quantum
circuit
by a quantum
circuit 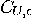 consisting of gates
from
consisting of gates
from 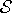 . Barenco and co-authors (see [4, 5
]) have proved that
. Barenco and co-authors (see [4, 5
]) have proved that 
| 1. | there is no
one-qubit universal gate,  |
| 2. | no classical
gate can be universal for quantum computing,  |
| 3. | 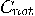 together with all single-bit
quantum gates form a universal set of gates for quantum computing. together with all single-bit
quantum gates form a universal set of gates for quantum computing.  |


