4.2 Feynman’s computer

Motivated by the construction
of universal reversible Boolean gates, Feynman [58, 59] proposed a quantum universal simulator
based on quantum versions of Boolean circuits. A quantum circuit is composed
of quantum wires and elementary quantum gates. Initially, Feynman’s approach
was seen as restrictive (see Deutsch _[48]), but in fact these two approaches
are equivalent. However, it took almost a decade to get the proof, see Yao
_[143]:every computation which can be performed efficiently
on a quantum Turing machine can be done by a quantum circuit and conversely.


Figure 12:
Richard Feynman

Feynman’s _construction uses a serial connection
of 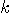 quantum gates, each performing a unitary
transformation. There are
quantum gates, each performing a unitary
transformation. There are  input/output
qubits and
input/output
qubits and 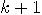 extra qubits as program counter
sites,
extra qubits as program counter
sites, 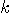 “creation" operators,
“creation" operators, 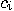 and
and 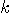 “annihilation" operators,
“annihilation" operators, 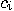 . A creation operator
. A creation operator 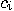 sets the
sets the 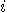 th
counter qubit to 1 and the annihilation operator
th
counter qubit to 1 and the annihilation operator 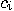 sets the
sets the 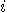 th
counter qubit to 0. These extra qubits are used to track the progress of
a computation. Only one program counter site is ever occupied, by the “cursor".
th
counter qubit to 0. These extra qubits are used to track the progress of
a computation. Only one program counter site is ever occupied, by the “cursor".

A computation starts by assigning the input bits into the input register
and the cursor to site 0. One checks if the site 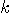 is empty or it has the cursor. When the cursor is found at the
is empty or it has the cursor. When the cursor is found at the
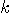 th site, we know that the entire circuit
has been used in the computation. At that time the state of the
th site, we know that the entire circuit
has been used in the computation. At that time the state of the  qubits has the answer to the computation.
qubits has the answer to the computation.

The quantum computer does not take care itself of termination! The time when
the measurement is to be performed has to be determined from outside.

Peres [109] has improved Feynman’s design in (a)
timing the end of calculation, (b) the analysis of possible errors (in the
program as well in measurements), and (c) extending the computation with
general qubit states 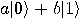 .
.







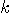 quantum gates, each performing a unitary
transformation. There are
quantum gates, each performing a unitary
transformation. There are  input/output
qubits and
input/output
qubits and 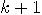 extra qubits as program counter
sites,
extra qubits as program counter
sites, 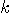 “creation" operators,
“creation" operators, 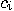 and
and 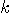 “annihilation" operators,
“annihilation" operators, 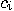 . A creation operator
. A creation operator 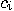 sets the
sets the 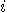 th
counter qubit to 1 and the annihilation operator
th
counter qubit to 1 and the annihilation operator 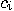 sets the
sets the 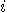 th
counter qubit to 0. These extra qubits are used to track the progress of
a computation. Only one program counter site is ever occupied, by the “cursor".
th
counter qubit to 0. These extra qubits are used to track the progress of
a computation. Only one program counter site is ever occupied, by the “cursor".

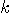 is empty or it has the cursor. When the cursor is found at the
is empty or it has the cursor. When the cursor is found at the
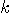 th site, we know that the entire circuit
has been used in the computation. At that time the state of the
th site, we know that the entire circuit
has been used in the computation. At that time the state of the  qubits has the answer to the computation.
qubits has the answer to the computation.


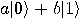 .
. 

