4.1 Benioff’s computer

Benioff [
10
] devised a hybrid Turing machine, in which a classical part co-exists with a quantum part. His model is a Turing machine with a tape consisting of a sequence of qubits (spin states), each one being in one of the basis state  or
or 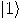 . The head of the machine was replaced by a quantum mechanical interaction that could “change" the values of qubits. The transition rules came from a specific Schr ödinger equation satisfying the following property: the initial configuration of spins evolves into a final set of spins which, when decoded as bits, will represent the result of the calculation. The program was encoded in the specific form of the Schr ödinger equation. The computation was done in steps of fixed duration so that at the end of each step the tape was back in one of the basis states
. The head of the machine was replaced by a quantum mechanical interaction that could “change" the values of qubits. The transition rules came from a specific Schr ödinger equation satisfying the following property: the initial configuration of spins evolves into a final set of spins which, when decoded as bits, will represent the result of the calculation. The program was encoded in the specific form of the Schr ödinger equation. The computation was done in steps of fixed duration so that at the end of each step the tape was back in one of the basis states  (representing 0) or
(representing 0) or 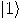 (representing 1), but during a computational step the machine could temporarily be in a superposition of spin states.
(representing 1), but during a computational step the machine could temporarily be in a superposition of spin states.

At the end of each step the head measured the state of the tape which destroyed all superpositions on the tape. Consequently, quantum interference was only partially used, in fact it was destroyed at the end of each step. Hence, a classical Turing machine could simulate easily such a computation.

Benioff’s machine faces at least two major problems, (a) the design of the Hamiltonian that mimics a specific Turing machine has to incorporate all computational paths performed by that specific machine (which, in a sense, amounts to knowing the answer of the problem you want to solve before actually running the computation), (b) the interactions between the head of the machine and its tape are difficult to realize because these physical objects can be far apart. The first problem was theoretically solved by Benioff, but the second one could not be solved.




 or
or 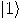 . The head of the machine was replaced by a quantum mechanical interaction that could “change" the values of qubits. The transition rules came from a specific Schr ödinger equation satisfying the following property: the initial configuration of spins evolves into a final set of spins which, when decoded as bits, will represent the result of the calculation. The program was encoded in the specific form of the Schr ödinger equation. The computation was done in steps of fixed duration so that at the end of each step the tape was back in one of the basis states
. The head of the machine was replaced by a quantum mechanical interaction that could “change" the values of qubits. The transition rules came from a specific Schr ödinger equation satisfying the following property: the initial configuration of spins evolves into a final set of spins which, when decoded as bits, will represent the result of the calculation. The program was encoded in the specific form of the Schr ödinger equation. The computation was done in steps of fixed duration so that at the end of each step the tape was back in one of the basis states  (representing 0) or
(representing 0) or 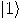 (representing 1), but during a computational step the machine could temporarily be in a superposition of spin states.
(representing 1), but during a computational step the machine could temporarily be in a superposition of spin states. 



