3.4 Measurements

The measurement of one or more particles in a quantum system results in a projection of the state of the system prior to measurement onto the subspace of the state space compatible with the measured values. The amplitude of the projection is rescaled to make sure that the resulting state vector has length one. The probability that the result of the measurement is a given value is the sum of the squares of the absolute values of the amplitudes of all components compatible with that value of the measurement.

A simple example of measurement in a two qubit system will illustrate the above points. Let’s fix the basis 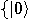 ,
, 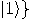 , and assume that all measurements of individual qubits will be done with respect to this basis. An arbitrary state of a two qubit system can be written as
, and assume that all measurements of individual qubits will be done with respect to this basis. An arbitrary state of a two qubit system can be written as

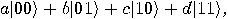
where 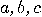 and
and  are complex numbers such that
are complex numbers such that

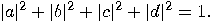
When the first qubit is measured, then the probability that the result is  is
is 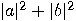 . Assume now that the measurement gives the first qubit exactly that value, that is,
. Assume now that the measurement gives the first qubit exactly that value, that is,  . Consequently, the state is projected onto the subspace compatible with the measurement which is the subspace spanned by
. Consequently, the state is projected onto the subspace compatible with the measurement which is the subspace spanned by 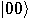 and
and 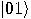 and the result of this projection is
and the result of this projection is 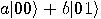 . Renormalizing we get:
. Renormalizing we get:

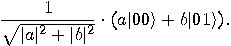
In general, consider a system containing  qubits
qubits 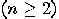 . Any state
. Any state 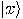 of the system can be expressed as
of the system can be expressed as

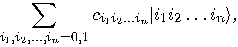
where

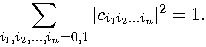
When the first qubit is measured with respect to the basis  , then the result
, then the result  is obtained with probability
is obtained with probability


After rescaling, the new state obtained after the measurement is

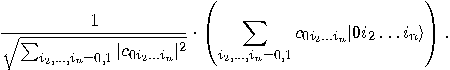
Similarly, the measurement gives the outcome 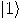 with the probability
with the probability


and the state changes correspondingly.

There are many speculations about the “collapse of the wave function (state)" due to an irreversible interaction of the microphysical quantum system with the macroscopic measurement apparatus. Some authors (see, for example, Greenberg and YaSin _[
65
] or Herzog, Kwiat, Weinfuter and Zeilinger _[
70
]) have argued that it is, in fact, possible to reconstruct the state of the physical system before the measurement, that is, to “reverse the collapse of the wave function" if the process of measurement is reversible. After “reconstruction" no information about the measurement is left.

The act of measurement gives another perspective about entangled particles. Particles are not entangled if the measurement of one has no effect on the other. For instance, the state


is entangled since the probability that the first bit is measured to be  is
is  if _the second bit has not been measured. However, if the second bit had been measured, then the probability that the first bit is measured as
if _the second bit has not been measured. However, if the second bit had been measured, then the probability that the first bit is measured as  is different from
is different from  , it is either 1 or 0, depending on whether the second bit was measured as
, it is either 1 or 0, depending on whether the second bit was measured as  or
or 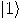 , respectively. Hence, the probability of measuring the first bit has been changed by the measurement of the second bit.
, respectively. Hence, the probability of measuring the first bit has been changed by the measurement of the second bit.

In contrast, the state

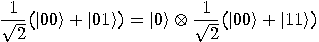
is not entangled. Reason: any measure of the first qubit will produce the result  independently whether a measurement is performed or not on the second qubit, and the second qubit has probability
independently whether a measurement is performed or not on the second qubit, and the second qubit has probability  to be measured to
to be measured to  regardless of whether the first qubit was measured or not.
regardless of whether the first qubit was measured or not.

In a sense, entangled states can be equivalently presented in mathematical terms (they cannot be represented as a tensor product of two states) or in physical terms (the measurement on one affects the other); however, the physical meaning is richer than the mathematical formalism.

An important consequence of the existence of entangled states is the fact that if a quantum memory register exists in an entangled state, one can change the state of one part of the register simply by measuring another part of it. This is a unique feature of quantum physics
 which has no parallel in classical physics. Entanglement is one of the most important features which distinguishes quantum from classical computing.
which has no parallel in classical physics. Entanglement is one of the most important features which distinguishes quantum from classical computing.


 Which is crucial in many quantum algorithms, teleportation, information transmission, etc.
Which is crucial in many quantum algorithms, teleportation, information transmission, etc.



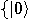 ,
, 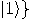 , and assume that all measurements of individual qubits will be done with respect to this basis. An arbitrary state of a two qubit system can be written as
, and assume that all measurements of individual qubits will be done with respect to this basis. An arbitrary state of a two qubit system can be written as 
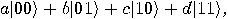
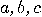 and
and  are complex numbers such that
are complex numbers such that 
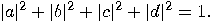
 is
is 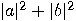 . Assume now that the measurement gives the first qubit exactly that value, that is,
. Assume now that the measurement gives the first qubit exactly that value, that is,  . Consequently, the state is projected onto the subspace compatible with the measurement which is the subspace spanned by
. Consequently, the state is projected onto the subspace compatible with the measurement which is the subspace spanned by 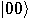 and
and 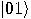 and the result of this projection is
and the result of this projection is 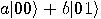 . Renormalizing we get:
. Renormalizing we get: 
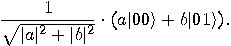
 qubits
qubits 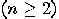 . Any state
. Any state 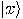 of the system can be expressed as
of the system can be expressed as 
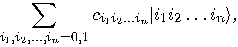

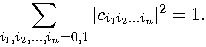
 , then the result
, then the result  is obtained with probability
is obtained with probability 


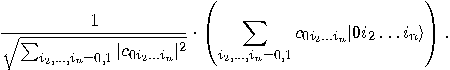
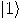 with the probability
with the probability 





 is
is  if _the second bit has not been measured. However, if the second bit had been measured, then the probability that the first bit is measured as
if _the second bit has not been measured. However, if the second bit had been measured, then the probability that the first bit is measured as  is different from
is different from  , it is either 1 or 0, depending on whether the second bit was measured as
, it is either 1 or 0, depending on whether the second bit was measured as  or
or 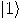 , respectively. Hence, the probability of measuring the first bit has been changed by the measurement of the second bit.
, respectively. Hence, the probability of measuring the first bit has been changed by the measurement of the second bit. 

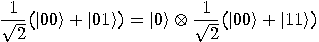
 independently whether a measurement is performed or not on the second qubit, and the second qubit has probability
independently whether a measurement is performed or not on the second qubit, and the second qubit has probability  to be measured to
to be measured to  regardless of whether the first qubit was measured or not.
regardless of whether the first qubit was measured or not. 

 which has no parallel in classical physics. Entanglement is one of the most important features which distinguishes quantum from classical computing.
which has no parallel in classical physics. Entanglement is one of the most important features which distinguishes quantum from classical computing. 

 Which is crucial in many quantum algorithms, teleportation, information transmission, etc.
Which is crucial in many quantum algorithms, teleportation, information transmission, etc.