3.3 The outlaw of copying

Quantum states cannot be cloned, as Wooters and Zurek _[
142
], and Dieks [
53
] have proved as a direct application of the linearity of unitary transformations. It is not possible to create the state 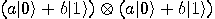 from an unknown state
from an unknown state 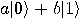 . In other words, there is no unitary transformation
. In other words, there is no unitary transformation 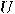 such that
such that 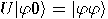 for all quantum states
for all quantum states 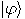 .
.

It’s important to understand that the no cloning principle states the impossibility of reliably cloning an unkown quantum state: it is possible to clone a known quantum state. It is possible to obtain  particles in an entangled state
particles in an entangled state 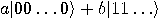 from an unknown state
from an unknown state 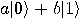 . Each particle will behave in exactly the same way when measured with respect to the basis
. Each particle will behave in exactly the same way when measured with respect to the basis 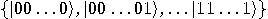 , but not when measured with respect to other bases. It is not possible to create the
, but not when measured with respect to other bases. It is not possible to create the  particle state
particle state

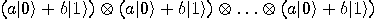
from an unkown state 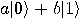 , cf. Rieffel and Polak [
117
].
, cf. Rieffel and Polak [
117
].

In a sense, the no cloning principle seems to announce “bad news": we lose one of the most important facilities of classical computation, the unlimited possibility to copy. There is “good news" derived from this principle, for example, the possibility of unconditional secure key generation (see Section 6.2 in Gruska _[
67
]). New techniques (see, for example, Buzek, Braunstein, Hillery, Bru , [
25
]) open possibilites to produce “approximate" copies of qubits: imperfect, but very close to real copies of qubits can be produced with a “quality" not depending upon the qubits to be copied. Of course, there is a price to be paid: copies produced in this way are entangled.
, [
25
]) open possibilites to produce “approximate" copies of qubits: imperfect, but very close to real copies of qubits can be produced with a “quality" not depending upon the qubits to be copied. Of course, there is a price to be paid: copies produced in this way are entangled.




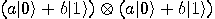 from an unknown state
from an unknown state 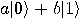 . In other words, there is no unitary transformation
. In other words, there is no unitary transformation 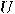 such that
such that 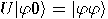 for all quantum states
for all quantum states 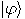 .
. 
 particles in an entangled state
particles in an entangled state 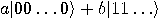 from an unknown state
from an unknown state 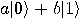 . Each particle will behave in exactly the same way when measured with respect to the basis
. Each particle will behave in exactly the same way when measured with respect to the basis 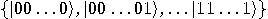 , but not when measured with respect to other bases. It is not possible to create the
, but not when measured with respect to other bases. It is not possible to create the  particle state
particle state 
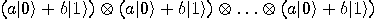
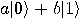 , cf. Rieffel and Polak [
117
].
, cf. Rieffel and Polak [
117
]. 
 , [
25
]) open possibilites to produce “approximate" copies of qubits: imperfect, but very close to real copies of qubits can be produced with a “quality" not depending upon the qubits to be copied. Of course, there is a price to be paid: copies produced in this way are entangled.
, [
25
]) open possibilites to produce “approximate" copies of qubits: imperfect, but very close to real copies of qubits can be produced with a “quality" not depending upon the qubits to be copied. Of course, there is a price to be paid: copies produced in this way are entangled. 

