|
|
|
|

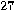 (see also the discussion in Calude, _Dinneen _and Svozil
_[36]).
(see also the discussion in Calude, _Dinneen _and Svozil
_[36]). 
 grams
heavier than normal ones. Can he find the odd stack by a single “weighting"?
A simple solution is the following:
grams
heavier than normal ones. Can he find the odd stack by a single “weighting"?
A simple solution is the following:

 |
Take one coin
from the first stack, two coins from the second stack, …, five coins from
the last stack.  |
 |
Measure the
weight of the combination of coins and obtain the number 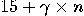 . .  |
 |
The  -th stack contains false coins. -th stack contains false coins.  |




 |
We have 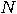 stacks of coins and we know that at most one stack may contain false coins. We are allowed to take just one coin from each stack.
Can we determine whether there is a stack containing false coins, and in
the affirmative, which? stacks of coins and we know that at most one stack may contain false coins. We are allowed to take just one coin from each stack.
Can we determine whether there is a stack containing false coins, and in
the affirmative, which?  |
 |
We have now
a countable many stacks, all of them, except at most one, containing true
coins only. Can we determine whether there is a stack containing false coins?
 |


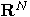 as quantum
space. Denote by
as quantum
space. Denote by  the weight
of a coin in the
the weight
of a coin in the 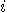 -th stack; if the
-th stack; if the 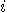 -th stack contains true coins, then
-th stack contains true coins, then  , otherwise,
, otherwise, 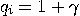 .
. 
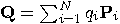 , where
, where 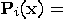
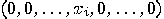 :
: 
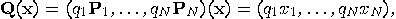
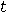 -th iteration of the operator
-th iteration of the operator 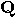 ,
, 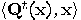 , and consider its dynamics:
, and consider its dynamics: 
 |
if all
coins are true  , for all , for all
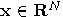 ; ;  |
 |
if there
are false coins in some stack, for some 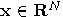 , , 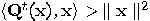 , and the
value increases with every new iteration. , and the
value increases with every new iteration.  |

 , for example, the Gaussian
distribution
, for example, the Gaussian
distribution 

 is the integral
is the integral 

 . The procedure will be probabilistic: it will indicate a method to decide, with a probability as close
to one as we want, whether there exist any false coins; in the affirmative
we will find the stack of false coins.
. The procedure will be probabilistic: it will indicate a method to decide, with a probability as close
to one as we want, whether there exist any false coins; in the affirmative
we will find the stack of false coins. 
 as
probability threshold. Assume that both
as
probability threshold. Assume that both 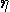 and
and  are computable reals. Choose a “test" vector
are computable reals. Choose a “test" vector 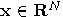 . Assume that we have a quantum “device" which
measures the quadratic form and clicks at time
. Assume that we have a quantum “device" which
measures the quadratic form and clicks at time  on
on 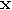 when
when 
 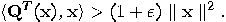 |
(14) |
 . In what follows we will
assume that
. In what follows we will
assume that 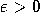 is a positive computable real.
is a positive computable real.


| 1. | If  then the “device" has clicked
at time then the “device" has clicked
at time  and we know for sure that
there exist false coins in the system. and we know for sure that
there exist false coins in the system.  |
| 2. | If at time
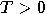 the “device" hasn’t (yet?) clicked,
then either all coins are true, i.e., the “device" hasn’t (yet?) clicked,
then either all coins are true, i.e.,  , for all , for all 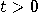 ,
or at time ,
or at time  the growth of the growth of  hasn’t yet reached the threshold hasn’t yet reached the threshold
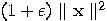 . .  |
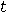 the test-vector
the test-vector 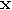 produces “true" information; we can call
produces “true" information; we can call 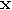 a “true" vector.
a “true" vector. 
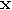 is
“lying" at time
is
“lying" at time  as we do have
false coins in the system, but they were not detected at time
as we do have
false coins in the system, but they were not detected at time  ; we say that
; we say that 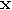 produces “false" information at time
produces “false" information at time  .
. 

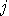 -th stack, then each test-vector
-th stack, then each test-vector
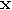 whose
whose 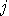 -th coordinate is 0 produces “false" information
at any time.
-th coordinate is 0 produces “false" information
at any time. 
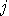 -th stack,
-th stack,  , but
, but 
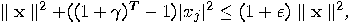
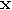 produces “false" information at time
produces “false" information at time
 . If
. If 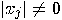 , then
, then 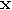 produces
“false" information only a finite period of time, that is, only for
produces
“false" information only a finite period of time, that is, only for 



 such that when presented a randomly chosen
test-vector
such that when presented a randomly chosen
test-vector 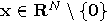 to a quantum
“device" with sensitivity
to a quantum
“device" with sensitivity  that fails to
click in time
that fails to
click in time  , then the system doesn’t
contain false coins with probability larger than
, then the system doesn’t
contain false coins with probability larger than 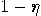 .
. 
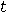

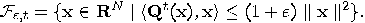
 , for all
, for all  . If there is one stack (say,
the
. If there is one stack (say,
the 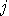 -th one) containing
false coins, then
-th one) containing
false coins, then 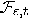 is a
cone
is a
cone 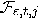 centered at the “false"
plane
centered at the “false"
plane  :
: 
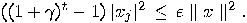

  |
(15) |

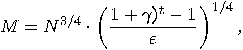

  |
(16) |

 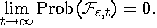 |
(17) |
 we can construct
the computable bound
we can construct
the computable bound 
 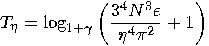 |
(18) |
 then we get
then we get 

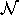 the event “the system contains no false coins"
and by
the event “the system contains no false coins"
and by  the event “the system
contains false coins". By
the event “the system
contains false coins". By 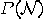 (
(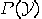 ) we denote
the a priori probability that the system contains no false coins
(the system contains false coins).
) we denote
the a priori probability that the system contains no false coins
(the system contains false coins). 
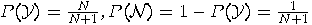 . We
can use Bayes’ formula to obtain the a
posteriori probability that the system contains only true coins when at time
. We
can use Bayes’ formula to obtain the a
posteriori probability that the system contains only true coins when at time
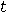 the quantum “device" didn’t click:
the quantum “device" didn’t click: 
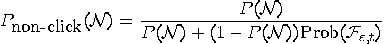
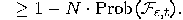
 ,
, 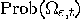 goes to
goes to  , so
, so
 goes to
goes to  . More precisely, if
. More precisely, if  as in (18), then
as in (18), then 
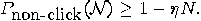

for every computable  we can construct a computable time we can construct a computable time  such that picking up at random
a test-vector such that picking up at random
a test-vector 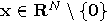 and using
a quantum “device" with sensitivity and using
a quantum “device" with sensitivity  up
to time up
to time  either either
|
 ) will distinguish the values of the iterated
quadratic form
) will distinguish the values of the iterated
quadratic form 

 corresponding to two discrete
stochastic processes. We will work with the intersections of
corresponding to two discrete
stochastic processes. We will work with the intersections of 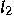 with the discrete Sobolev class
with the discrete Sobolev class
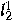 of summable sequences with
the square norm square norm
of summable sequences with
the square norm square norm 

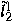 of weighted-summable sequences with the square norm
of weighted-summable sequences with the square norm 

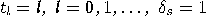 and to the perturbed sequence of
moments of time
and to the perturbed sequence of
moments of time 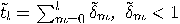 .
. 
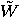 and
and 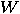 on these spaces and use the following relation between
on these spaces and use the following relation between 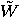 and
and 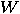 : for
every
: for
every 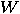 –measurable set
–measurable set  ,
, 


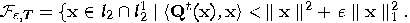
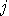 , then _
, then _


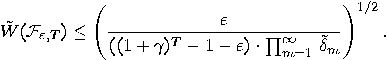



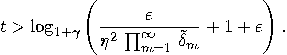


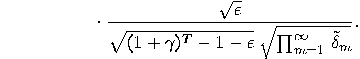


 which will be used by our quantum device to
run the experiment on the random test-vector. This is possible because the
set of “lying test-vectors" has constructive measure zero. If the device
clicks in time
which will be used by our quantum device to
run the experiment on the random test-vector. This is possible because the
set of “lying test-vectors" has constructive measure zero. If the device
clicks in time  then the
answer is “the programs stops"; otherwise, the answer is “the program doesn’t
stop with the pre-given accuracy".
then the
answer is “the programs stops"; otherwise, the answer is “the program doesn’t
stop with the pre-given accuracy". 

 |
Not
surprisingly, our approach goes beyond the “classical" model of quantum Turing
machine.  |
 |
The main result is mathematical:
the Wiener measure of the indistinguishable
set  constructively tends to zero when constructively tends to zero when  tends to infinity. tends to infinity.  |
 |
The main ingredients of our approach are: a special
type of continuity, the choice of test-vectors from a special class of trajectories
of two Markov processes working in two different scales of time and realized
as elements of an infinitely-dimensional Hilbert space (infinite superposition),
the ability to work with “truly random" test-vectors in an evolution described
by an exponentially growing semigroup and the possibility to obtain the result
from a single measurement.  |
 |
At this stage
the “device" is more mathematical than physical. The discrete-time Brownian
motion–used in the estimation of the probability of the indistinguishable
set in the last section–can be represented as a “sum" of independent random
variables with Gaussian distributions. It can be implemented as a “sum" of
spins of a cascade of electrons formed by the shock-induced emission on a
special geometrical structure of semiconductor elements with special random
properties  |
 |
Many problems
are still open and much more remains to be done. Is the method used
in this paper “natural"? Is it feasible? Is it better or can we get more
“insight" about the nature of the Halting Problem if we use unitary operators?
 |

 For other approaches see the relativistic computing
by Etesi and Németi [57] based on Hogart [73] and Kieu [79]
For other approaches see the relativistic computing
by Etesi and Németi [57] based on Hogart [73] and Kieu [79]