|
|
|
|



Yet, if the segment of length 1 really consists of infinitely many subsegments of length 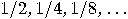 , as of ‘chopped-off’ wholes, then it is incompatible with the character of the infinite as the ‘incompletable’ that Achilles should have been able to traverse them all. If one admits this possibility, then there is no reason why a machine should not be capable of completing an infinite sequence of distinct acts of decision within a finite amount of time; say, by supplying the first result after , as of ‘chopped-off’ wholes, then it is incompatible with the character of the infinite as the ‘incompletable’ that Achilles should have been able to traverse them all. If one admits this possibility, then there is no reason why a machine should not be capable of completing an infinite sequence of distinct acts of decision within a finite amount of time; say, by supplying the first result after  minute, the second after another minute, the second after another 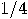 minute, the third minute, the third 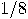 minute later than the second, etc. In this way it would be possible, provided the receptive power of the brain would function similarly, to achieve a traversal of all natural numbers and thereby a sure yes-or-no decision regarding any existential question about natural numbers! minute later than the second, etc. In this way it would be possible, provided the receptive power of the brain would function similarly, to achieve a traversal of all natural numbers and thereby a sure yes-or-no decision regarding any existential question about natural numbers!

|
 and
and 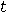 as follows:
as follows:

 |
The proper time 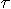 measures the physical system time by clocks in an usual way. measures the physical system time by clocks in an usual way.
 |
 |
A discrete cycle time 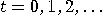 characterizes an “intrinsic" time scale for a process running on the machine. characterizes an “intrinsic" time scale for a process running on the machine.
 |
 |
For some unspecified reason we assume that the machine allows us to “squeeze" its intrinsic time 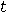 with respect to the proper time with respect to the proper time 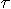 by a geometric progression. For by a geometric progression. For 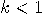 we let any time cycle of we let any time cycle of 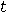 , if measured in terms of , if measured in terms of 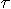 , to be “squeezed" by a factor of , to be “squeezed" by a factor of 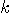 with respect to the foregoing time cycle. More precisely, with respect to the foregoing time cycle. More precisely, 


|
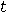 approaches the infinity, the proper time
approaches the infinity, the proper time 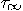 approaches
approaches 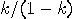 , so it remains finite.
, so it remains finite. 
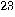 One might argue that such an “oracle" would require a geometric energy increase resulting in an infinite consumption of energy. Yet, no currently accepted classical physical principle excludes us from assuming that every geometric decrease in cycle time could be associated with a geometric progression in energy consumption, at least up to some limiting (e.g. Planck) scale.
One might argue that such an “oracle" would require a geometric energy increase resulting in an infinite consumption of energy. Yet, no currently accepted classical physical principle excludes us from assuming that every geometric decrease in cycle time could be associated with a geometric progression in energy consumption, at least up to some limiting (e.g. Planck) scale. 
 whose input is a binary string
whose input is a binary string 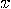 . Assume, for the sake of a contradiction, that there exists an effective halting algorithm HALT, implementable on a Zeno machine, which is able to decide whether
. Assume, for the sake of a contradiction, that there exists an effective halting algorithm HALT, implementable on a Zeno machine, which is able to decide whether 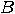 eventually stops on
eventually stops on 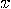 or not. Using HALT
or not. Using HALT we shall construct another Zeno machine
we shall construct another Zeno machine  , which has as an input a program
, which has as an input a program 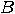 and which proceeds as follows: Upon reading the program
and which proceeds as follows: Upon reading the program 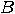 as an input,
as an input,  makes a copy of it.
makes a copy of it.
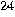 In the next step, our machine uses the code
In the next step, our machine uses the code 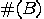 as an input string for
as an input string for 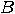 itself, that is,
itself, that is,  forms
forms 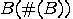 , henceforth denoted by
, henceforth denoted by 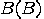 . The machine hands
. The machine hands 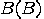 over to its subroutine HALT. Then,
over to its subroutine HALT. Then,  proceeds as follows:
proceeds as follows:

 |
if HALT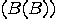 decides that decides that 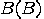 eventually halts, then eventually halts, then  does not halt, does not halt,

 |
 |
if HALT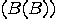 decides that decides that 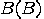 never halts, then never halts, then  halts. halts.

|
 on its own code as input? Notice that
on its own code as input? Notice that 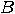 is arbitrary, so there is no restriction to prevent us for doing this! Consequently,
is arbitrary, so there is no restriction to prevent us for doing this! Consequently,  , which is representable by its code
, which is representable by its code  will be applied to itself.
will be applied to itself. 
 is restricted to classical bits of information. Then, whenever
is restricted to classical bits of information. Then, whenever  halts, HALT
halts, HALT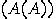 forces
forces  not to halt, and conversely, whenever
not to halt, and conversely, whenever  does not halt, then HALT
does not halt, then HALT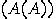 steers
steers  into the halting state. In both cases one arrives at a contradiction, therefore, Zeno machines are logically inconsistent.
into the halting state. In both cases one arrives at a contradiction, therefore, Zeno machines are logically inconsistent. 
 is allowed a qubit _of information. Assume that
is allowed a qubit _of information. Assume that  and
and 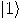 are the halting and nonhalting states, respectively. The computation can be performed if
are the halting and nonhalting states, respectively. The computation can be performed if  receives as an input a qubit corresponding to the fixed point state
receives as an input a qubit corresponding to the fixed point state 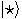 of the NOT operator
of the NOT operator
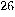 :
: 
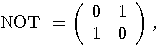
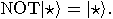

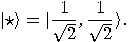
 proves the impossibility of
proves the impossibility of  to control the output as the probability to reach a halting (nonhalting) state is exactly one half. At the level of probability amplitudes, quantum theory permits Zeno machines, but at the level of observable probabilities, this super-power is nullified, as the result of the computation appears to be random.
to control the output as the probability to reach a halting (nonhalting) state is exactly one half. At the level of probability amplitudes, quantum theory permits Zeno machines, but at the level of observable probabilities, this super-power is nullified, as the result of the computation appears to be random. 

 Classical mechanics postulates space and time continua as a foundational principle.
Classical mechanics postulates space and time continua as a foundational principle. This can be readily achieved, since the program
This can be readily achieved, since the program 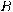 is presented to
is presented to 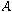 in some encoded form
in some encoded form  , i.e. as a string of symbols.
, i.e. as a string of symbols.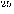 This can be realized by an infinite loop.
This can be realized by an infinite loop.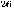 Diagonalization operator.
Diagonalization operator.