6 Quantum Cryptography

Quantum systems can be used to
achieve cryptographic tasks, such as secret (secure) communication. In cryptography
(see, for example, Salomaa _[119]) it is
very difficult, if not impossible, to prove by experiment that a cryptographic
protocol is secure: who knows whether an eavesdropper (spy, competitor) managed
to beat the system? For example, the bit-commitment method, thought for a
while to be secure through quantum methods, was proven to be insecure, cf.
Mayers _[95
] and Lo, Chau _[90].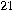 The only confidence one can hope to achieve
relies on mathematical arguments, the so-called proofs of security.
The only confidence one can hope to achieve
relies on mathematical arguments, the so-called proofs of security.

As usual in quantum mechanics scenarios, Alice and Bob are widely separated
and wish to communicate. They are connected by an ordinary bi-directional
open channel and a uni-directional quantum channel, directed from Alice to
Bob. The quantum channel allows Alice to send single qubits (e.g. photons)
to Bob who can measure their quantum state. An eavesdropper, Eve, is able
to intercept and measure the qubits, then pass them on to Bob.

Given two orthonormal bases


where 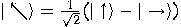 and
and 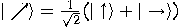 , Alice and Bob can agree to
associate
, Alice and Bob can agree to
associate  and
and 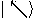 with
with  ,
, 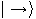 and
and 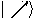 with
with  . For each bit, Alice pseudo-randomly uses
one of these bases and Bob also pseudo-randomly selects a basis for measuring
the received qubit. After the bits have been transmitted, Alice and Bob inform
each other (using the open channel) of the basis they used to prepare and
measure each qubit. In this way, they find out when they used the same
basis, which happens on average half of the time, and retain only those results.
. For each bit, Alice pseudo-randomly uses
one of these bases and Bob also pseudo-randomly selects a basis for measuring
the received qubit. After the bits have been transmitted, Alice and Bob inform
each other (using the open channel) of the basis they used to prepare and
measure each qubit. In this way, they find out when they used the same
basis, which happens on average half of the time, and retain only those results.

If Eve measures the qubits transmitted by Alice, then she uses the correct
basis on average half of the time. Therefore, assuming that  qubits are sent by Alice,
qubits are sent by Alice,  bits are received by Bob without any disturbance.
In
bits are received by Bob without any disturbance.
In  cases, Bob will also
use the correct basis.
cases, Bob will also
use the correct basis.

What about the other  qubits sent by Alice?
Since
qubits sent by Alice?
Since

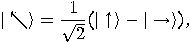
and

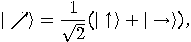
the probability to find a qubit represented by the state 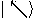 or
or 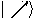 in the state
in the state 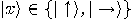 is
is

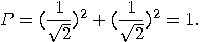
Taking into account that

the same result will be obtained by interchanging the two bases. Consequently,
if  qubits are disturbed by Eve, then half
of them are measured by Bob with the correct basis and
qubits are disturbed by Eve, then half
of them are measured by Bob with the correct basis and  qubits will be projected by
Bob’s measurement back onto original state. Eve’s tentative interception
disturbs only a quarter of the message retained by Bob. Alice and Bob can
now detect Eve’s presence by pseudo-randomly choosing
qubits will be projected by
Bob’s measurement back onto original state. Eve’s tentative interception
disturbs only a quarter of the message retained by Bob. Alice and Bob can
now detect Eve’s presence by pseudo-randomly choosing  bits of the string and announcing
over the open channel the values they have. If they agree on all these bits,
then the probability that no eavesdropper was present is
bits of the string and announcing
over the open channel the values they have. If they agree on all these bits,
then the probability that no eavesdropper was present is  . The undisclosed bits represent
the “secret key".
. The undisclosed bits represent
the “secret key".

The above scenario is extremely “theoretical", as it assumes that one possible
strategy for Eve – she may deliberately not intercept all qubits (after all,
she knows everything about quantum key distribution, doesn’t she?). Noise
may influence the trio “communication" as well. There are various subtle
methods to address these issues, but we are not going to enter into details
(see, for example, Gruska _[67]). It is important to observe that variants
of the quantum key distribution are
feasible with current technology.

In what follows we will illustrate the use of quantum gates for to obtain
the so-called “quantum teleportation", that is transmitting qubits without
sending qubits!

What does this mean? Is it a pun? According to Bennett, (a co-author of a
1993 paper that proposed quantum teleportation, [17]) “It’s a means by which you can
take apart an unknown quantum state into classical information and purely
quantum information, send them through two separate channels, put them back
together, and get back the original quantum state".

Teleportation, as it is commonly understood, is a fictional procedure of
transferring an object from one location to another location in a three stage
process: (a) dissociation, (b) information transmission, (c) reconstitution.
The point is that, in contrast with fax transmission – where the original
object remains intact at the initial location, only an approximate replica
is constructed at destination, in teleportation the original object is distroyed
after enough information about it has been extracted, the object is not traversing
in any way the space between locations, but it is reconstructed, as an exact
replica, at the destination.

Quantum teleportation allows for the transmission of quantum information
to a distant location. The objective is to transmit the quantum state of
a particle using classical bits and reconstruct the state at the receiver.

Let’s assume that Alice wishes to communicate with Bob a single qubit in
an unkown state  ; she wants
to make the transmission through classical channels. Alice cannot know with
certainty the state as any measurement she may perform may change it; she
cannot clone it because of the no cloning result! So, it seems that the only
way to send Bob the qubit is to send him the physical qubit, or to
swap the state into another quantum system and then send Bob that system.
; she wants
to make the transmission through classical channels. Alice cannot know with
certainty the state as any measurement she may perform may change it; she
cannot clone it because of the no cloning result! So, it seems that the only
way to send Bob the qubit is to send him the physical qubit, or to
swap the state into another quantum system and then send Bob that system.


Figure 18: Teleportation group
As with dense coding, they use an entangled pair


Alice controls the first half of the pair and Bob controls the
second one. The input state is



Alice now applies the transformation  to this state. The third bit is left unchanged;
only the first two bits belong to Alice and the rightmost one belongs to
Bob.
to this state. The third bit is left unchanged;
only the first two bits belong to Alice and the rightmost one belongs to
Bob.

Applying now 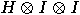 , we obtain
, we obtain




Alice then measures her two qubits, obtaining four possible results: 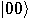 ,
, 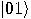 ,
,  , or
, or 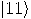 with equal
probability 1/4. Depending on the result of the measurement, the quantum
state of Bob’s qubit is projected to
with equal
probability 1/4. Depending on the result of the measurement, the quantum
state of Bob’s qubit is projected to 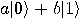 ,
, 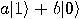 ,
, 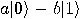 ,
, 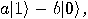 respectively. Alice sends the
result of her measurement as two classical bits to Bob. He will know what
has happened, and can apply the decoding transformation
respectively. Alice sends the
result of her measurement as two classical bits to Bob. He will know what
has happened, and can apply the decoding transformation 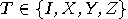 to fix his qubit.
to fix his qubit.

The final output state is 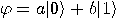 , which, as desired, is the unknown qubit that Alice wanted to
send.
, which, as desired, is the unknown qubit that Alice wanted to
send.

Recently, important teleportation experiments have been performed in Innsbruck
and Caltech: for a recent report see Bouwmeester, _Pan,
_Weinfurter, _Zeilinger
_[21]. There is a lot of controversy about the nature
of quantum teleportation and what criteria should be met by a successful
experiment. The following criteria for evaluating a quantum teleportation
procedure have been proposed in [21]:
| Received
bits |
State
|
Transformation |
Result
|
| 00
|
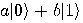 |
I |
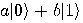 |
| 01 |
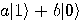 |
X |
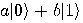 |
| 10 |
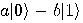 |
Z |
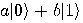 |
| 11 |
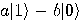 |
Y |
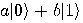 |
Table 7: An
illustration of quantum teleportation
 How well can it teleport any arbitrary quantum state
it is intended to teleport? (fidelity of teleportation)
How well can it teleport any arbitrary quantum state
it is intended to teleport? (fidelity of teleportation)

 How often does
it succeed to teleport, when it is given an input state within the set of
states it is designed to teleport? (efficiency of teleportation)
How often does
it succeed to teleport, when it is given an input state within the set of
states it is designed to teleport? (efficiency of teleportation)

 If given a
state the scheme is not intended to teleport, how well does it reject such
a state? (cross-talk rejection efficiency)
If given a
state the scheme is not intended to teleport, how well does it reject such
a state? (cross-talk rejection efficiency)
 Let us
close this section with another controversial statement of the same Bennett:
_“I think it’s quite clear that anything approximating
teleportation of complex living beings, even bacteria, is so far away technologically
that it’s not really worth thinking about it."
Let us
close this section with another controversial statement of the same Bennett:
_“I think it’s quite clear that anything approximating
teleportation of complex living beings, even bacteria, is so far away technologically
that it’s not really worth thinking about it."

 Cheating is possible through
a clever use of quantum entanglement.
Cheating is possible through
a clever use of quantum entanglement.


 The only confidence one can hope to achieve
relies on mathematical arguments, the so-called proofs of security.
The only confidence one can hope to achieve
relies on mathematical arguments, the so-called proofs of security. 



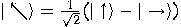 and
and 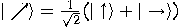 , Alice and Bob can agree to
associate
, Alice and Bob can agree to
associate  and
and 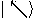 with
with  ,
, 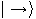 and
and 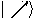 with
with  . For each bit, Alice pseudo-randomly uses
one of these bases and Bob also pseudo-randomly selects a basis for measuring
the received qubit. After the bits have been transmitted, Alice and Bob inform
each other (using the open channel) of the basis they used to prepare and
measure each qubit. In this way, they find out when they used the same
basis, which happens on average half of the time, and retain only those results.
. For each bit, Alice pseudo-randomly uses
one of these bases and Bob also pseudo-randomly selects a basis for measuring
the received qubit. After the bits have been transmitted, Alice and Bob inform
each other (using the open channel) of the basis they used to prepare and
measure each qubit. In this way, they find out when they used the same
basis, which happens on average half of the time, and retain only those results.

 qubits are sent by Alice,
qubits are sent by Alice,  bits are received by Bob without any disturbance.
In
bits are received by Bob without any disturbance.
In  cases, Bob will also
use the correct basis.
cases, Bob will also
use the correct basis. 
 qubits sent by Alice?
Since
qubits sent by Alice?
Since 
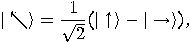

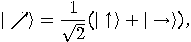
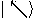 or
or 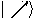 in the state
in the state 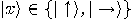 is
is 
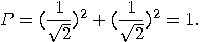

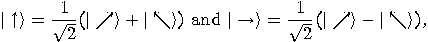
 qubits are disturbed by Eve, then half
of them are measured by Bob with the correct basis and
qubits are disturbed by Eve, then half
of them are measured by Bob with the correct basis and 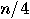 qubits will be projected by
Bob’s measurement back onto original state. Eve’s tentative interception
disturbs only a quarter of the message retained by Bob. Alice and Bob can
now detect Eve’s presence by pseudo-randomly choosing
qubits will be projected by
Bob’s measurement back onto original state. Eve’s tentative interception
disturbs only a quarter of the message retained by Bob. Alice and Bob can
now detect Eve’s presence by pseudo-randomly choosing  bits of the string and announcing
over the open channel the values they have. If they agree on all these bits,
then the probability that no eavesdropper was present is
bits of the string and announcing
over the open channel the values they have. If they agree on all these bits,
then the probability that no eavesdropper was present is  . The undisclosed bits represent
the “secret key".
. The undisclosed bits represent
the “secret key". 





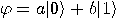 ; she wants
to make the transmission through classical channels. Alice cannot know with
certainty the state as any measurement she may perform may change it; she
cannot clone it because of the no cloning result! So, it seems that the only
way to send Bob the qubit is to send him the physical qubit, or to
swap the state into another quantum system and then send Bob that system.
; she wants
to make the transmission through classical channels. Alice cannot know with
certainty the state as any measurement she may perform may change it; she
cannot clone it because of the no cloning result! So, it seems that the only
way to send Bob the qubit is to send him the physical qubit, or to
swap the state into another quantum system and then send Bob that system.





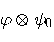

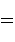

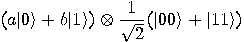






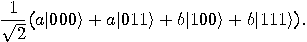




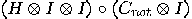 to this state. The third bit is left unchanged;
only the first two bits belong to Alice and the rightmost one belongs to
Bob.
to this state. The third bit is left unchanged;
only the first two bits belong to Alice and the rightmost one belongs to
Bob.
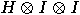 , we obtain
, we obtain 


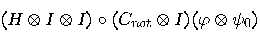

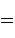

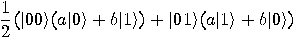







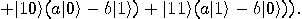




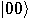 ,
, 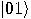 ,
,  , or
, or 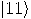 with equal
probability 1/4. Depending on the result of the measurement, the quantum
state of Bob’s qubit is projected to
with equal
probability 1/4. Depending on the result of the measurement, the quantum
state of Bob’s qubit is projected to 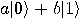 ,
, 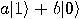 ,
, 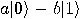 ,
, 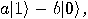 respectively. Alice sends the
result of her measurement as two classical bits to Bob. He will know what
has happened, and can apply the decoding transformation
respectively. Alice sends the
result of her measurement as two classical bits to Bob. He will know what
has happened, and can apply the decoding transformation 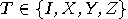 to fix his qubit.
to fix his qubit. 
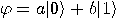 , which, as desired, is the unknown qubit that Alice wanted to
send.
, which, as desired, is the unknown qubit that Alice wanted to
send.
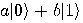
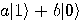
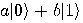
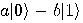
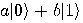
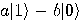
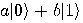
 How well can it teleport any arbitrary quantum state
it is intended to teleport? (fidelity of teleportation)
How well can it teleport any arbitrary quantum state
it is intended to teleport? (fidelity of teleportation) 
 How often does
it succeed to teleport, when it is given an input state within the set of
states it is designed to teleport? (efficiency of teleportation)
How often does
it succeed to teleport, when it is given an input state within the set of
states it is designed to teleport? (efficiency of teleportation) 
 If given a
state the scheme is not intended to teleport, how well does it reject such
a state? (cross-talk rejection efficiency)
If given a
state the scheme is not intended to teleport, how well does it reject such
a state? (cross-talk rejection efficiency)  Let us
close this section with another controversial statement of the same Bennett:
_“I think it’s quite clear that anything approximating
teleportation of complex living beings, even bacteria, is so far away technologically
that it’s not really worth thinking about it."
Let us
close this section with another controversial statement of the same Bennett:
_“I think it’s quite clear that anything approximating
teleportation of complex living beings, even bacteria, is so far away technologically
that it’s not really worth thinking about it." 
 Cheating is possible through
a clever use of quantum entanglement.
Cheating is possible through
a clever use of quantum entanglement.