|
|
|
|

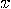 such that
such that
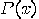 is true", where
is true", where 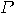 is an appropriate predicate. For example:
is an appropriate predicate. For example:

| (a) | Given an
 element vector element vector  , find a permutation , find a permutation  of of  such that for all such that for all 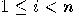 we have we have 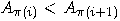 . .  |
| (b) | Given a graph
 with with  vertices vertices 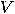 and and  edges edges 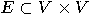 , and a set of , and a set of 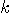 colours colours 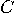 , find a colouring
map , find a colouring
map  from from 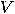 to to 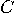 such that for all such that for all 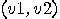 in in 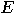 , ,  . .  |

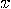 satisfying
satisfying 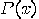 .
It is easily proven that there can be, in general, no shortcuts, so randomly
testing the predicate
.
It is easily proven that there can be, in general, no shortcuts, so randomly
testing the predicate 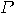 seems the best strategy
that can be adopted on a conventional computer. For a search space of size
seems the best strategy
that can be adopted on a conventional computer. For a search space of size
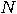 , the general unstructured search problem
is of complexity O(
, the general unstructured search problem
is of complexity O(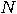 ), once the time it
takes to test the predicate
), once the time it
takes to test the predicate 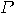 is factored
out. When we said “no shortcuts are possible in general" we meant “no shortcuts
are possible if we use conventional computers". However, Grover _[66] showed that
the unstructured search problem can
be solved with bounded probability
within O(
is factored
out. When we said “no shortcuts are possible in general" we meant “no shortcuts
are possible if we use conventional computers". However, Grover _[66] showed that
the unstructured search problem can
be solved with bounded probability
within O(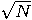 ) time with a quantum
computer.
) time with a quantum
computer. 
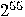 keys before hitting the right one, an operation
that takes more than 1 year even if one billion keys are checked every second.
By comparison, Grover’s algorithm can solve the problem, after quantum-DES
enciphering the known clear text, in just 185 million times. Hence, Grover’s
quantum searching algorithm can “in principle" be used to break classical
cryptographic systems such as DES.
keys before hitting the right one, an operation
that takes more than 1 year even if one billion keys are checked every second.
By comparison, Grover’s algorithm can solve the problem, after quantum-DES
enciphering the known clear text, in just 185 million times. Hence, Grover’s
quantum searching algorithm can “in principle" be used to break classical
cryptographic systems such as DES. 

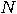 to find one item satisfying a given condition. It is assumed that it is easy
to check whether an arbitrary element satisfies the given condition. Let
to find one item satisfying a given condition. It is assumed that it is easy
to check whether an arbitrary element satisfies the given condition. Let
 be such that
be such that 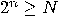 . Assume that predicate
. Assume that predicate 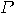 is implemented by a quantum gate
is implemented by a quantum gate 
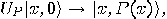

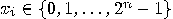 .
.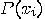 on this
register.
on this
register. to
to 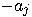 , for all
, for all
 such that
such that 
 with
with 
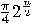 times.
times.
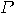 for all possible inputs
for all possible inputs  can be done by applying
can be done by applying 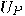 to a register containing the
superposition
to a register containing the
superposition 
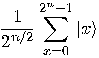

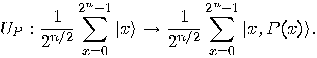

 such that
such that 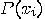 is true,
is true, 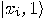 will be part of the result
superposition, but chances are very slim to get it via measurement,
will be part of the result
superposition, but chances are very slim to get it via measurement, 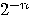 , since its amplitude is
, since its amplitude is  . The “trick" is to change the
resulting quantum state in such a way to greatly increase the amplitude of
all vectors
. The “trick" is to change the
resulting quantum state in such a way to greatly increase the amplitude of
all vectors 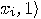 , for which
the predicate is true, and decrease the amplitude of vectors
, for which
the predicate is true, and decrease the amplitude of vectors 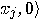 , for which the predicate is
false. This change in amplitudes is obtained using the inversion about the
average transformation; it can be accomplished with O(
, for which the predicate is
false. This change in amplitudes is obtained using the inversion about the
average transformation; it can be accomplished with O(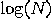 ) quantum gates.
) quantum gates. 

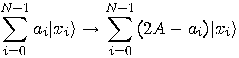
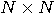 unitary matrix
unitary matrix 

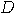 can be defined as
can be defined as 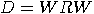 where
where 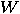 is the Walsh–Hdamard
transformation and
is the Walsh–Hdamard
transformation and  is the matrix:
is the matrix: 
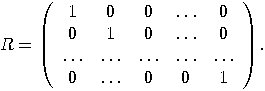

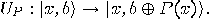
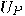 the superposition
the superposition 



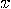 with
with 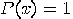 has been changed, but
has been changed, but  is unchanged.
is unchanged. 
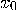 such that
such that  is true, then after
is true, then after 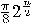 iterations of steps 2 through
4 the failure rate is
iterations of steps 2 through
4 the failure rate is  .
After iterating
.
After iterating 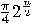 times the
failure rate drops to
times the
failure rate drops to 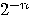 . For a more detailed
analysis see Gruska _[67].
. For a more detailed
analysis see Gruska _[67]. 
 iterations, the failure rate is close to 1. This
is an important feature of many quantum algorithms, which has little counterpart
in conventional computing. Repeating quantum procedures may improve results
for a while, but after some repetitions the results will get worse again.
Quantum procedures are unitary transformations, which are rotations of complex
space; repeated applications of a quantum transform may rotate the state
closer and closer to the desired state for a while, but eventually it will
rotate past the desired state to get further and further from the desired
state. Thus to obtain useful results from a repeated application of a quantum
transformation, it is paramount to know when to stop.
iterations, the failure rate is close to 1. This
is an important feature of many quantum algorithms, which has little counterpart
in conventional computing. Repeating quantum procedures may improve results
for a while, but after some repetitions the results will get worse again.
Quantum procedures are unitary transformations, which are rotations of complex
space; repeated applications of a quantum transform may rotate the state
closer and closer to the desired state for a while, but eventually it will
rotate past the desired state to get further and further from the desired
state. Thus to obtain useful results from a repeated application of a quantum
transformation, it is paramount to know when to stop. 

