|
|
|
|

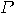 we can associate in a natural way the proposition
we can associate in a natural way the proposition

“the physical
system has property 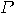 ", ",  |

“if the observable
is measured, then the property 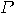 is observed". is observed".
 |

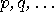 are associated with closed linear subspaces of
a Hilbert space through the origin (zero vector); the implication relation
are associated with closed linear subspaces of
a Hilbert space through the origin (zero vector); the implication relation
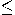 is associated with the set-theoretical
subset relation
is associated with the set-theoretical
subset relation  , and the logical or
, and the logical or 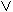 , and
, and 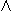 , and
not
, and
not  operations are associated with the
set-theoretic intersection
operations are associated with the
set-theoretic intersection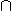 , the linear
span
, the linear
span  of subspaces and the orthogonal subspace
of subspaces and the orthogonal subspace
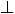 , respectively. The negation of
, respectively. The negation of 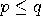 is denoted by
is denoted by 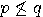 . The logical statement
. The logical statement  which is always true is identified with the
entire Hilbert space
which is always true is identified with the
entire Hilbert space 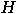 , and its complement
, and its complement
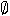 with the zero-dimensional subspace (zero
vector).
with the zero-dimensional subspace (zero
vector). 


 and
and 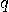 are orthogonal if
are orthogonal if 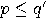 . Two propositions
. Two propositions 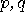 are co-measurable (compatible,
commuting) if there exist three mutually
orthogonal propositions
are co-measurable (compatible,
commuting) if there exist three mutually
orthogonal propositions 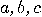 such that
such that 
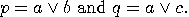
 and
and 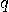 consist
of an “identical part"
consist
of an “identical part"  and two orthogonal
parts
and two orthogonal
parts  . Clearly, orthogonality
implies co-measurability, since if
. Clearly, orthogonality
implies co-measurability, since if  and
and 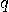 are orthogonal,
we may take
are orthogonal,
we may take 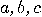 to be
to be  , respectively.
, respectively. 
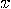 -axis.
-axis. There are two possible spin components of the particle,
There are two possible spin components of the particle,
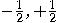 , which can be codified
as
, which can be codified
as 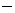 and
and  . The corresponding elementary propositions are:
. The corresponding elementary propositions are: 
 |
 = “the particle is in state = “the particle is in state
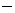 " = one-dimensional subspace spanned
by the vector " = one-dimensional subspace spanned
by the vector 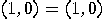 , and , and  |
 |
 = “the particle is in state = “the particle is in state
 " = one-dimensional subspace spanned
by the vector " = one-dimensional subspace spanned
by the vector 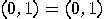 . .  |
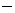 or in state
or in state  ", which is the whole space, and the absurdity
0 is the proposition “the particle is neither in state
", which is the whole space, and the absurdity
0 is the proposition “the particle is neither in state 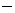 nor in state
nor in state  ", which is the zero-dimensional subspace of
", which is the zero-dimensional subspace of 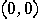 which is
which is 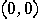 . The propositional structure
obtained in this case is the classical Boolean algebra with two elements;
its Hasse diagram appears in Figure 10
. Recall that in a Hasse diagram propositions are represented by dots, implication
is represented “vertically", that is
. The propositional structure
obtained in this case is the classical Boolean algebra with two elements;
its Hasse diagram appears in Figure 10
. Recall that in a Hasse diagram propositions are represented by dots, implication
is represented “vertically", that is 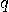 is drawn higher than
is drawn higher than  if
if 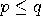 , and the propositions
, and the propositions  and
and 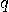 are connected
by a line.
are connected
by a line. 
 elements, so the so-called blocks in case of a Hilbert
space of dimension
elements, so the so-called blocks in case of a Hilbert
space of dimension  . However, non-co-measurable
observables should be treated as well! Of course, we may take the view that
non-co-measurable observables make no physical sense, so we should forget
about them (at least, with respect to current day knowledge; maybe, a “more
complete" theory could make sense of them!). This legitimate, but somewhat
“minority" position goes beyond our aim, so we will concentrate on the mainstream
approach which considers that non-co-measurable observables make physical
sense at least as theoretical constructions. Note that this attitude is common
also in mathematics, where, for example,
. However, non-co-measurable
observables should be treated as well! Of course, we may take the view that
non-co-measurable observables make no physical sense, so we should forget
about them (at least, with respect to current day knowledge; maybe, a “more
complete" theory could make sense of them!). This legitimate, but somewhat
“minority" position goes beyond our aim, so we will concentrate on the mainstream
approach which considers that non-co-measurable observables make physical
sense at least as theoretical constructions. Note that this attitude is common
also in mathematics, where, for example, 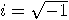 makes no “direct" sense, but proves to be extremely
useful.
makes no “direct" sense, but proves to be extremely
useful. 

 |
identify all
tautologies in all blocks,  |
 |
identify all
absurdities in all blocks,  |
 |
identify identical
elements in different blocks,  |
 |
keep intact
the logical structure of all blocks.  |
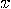 –axis
–axis 
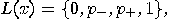
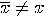 (mod
(mod  ), an identical
propositional system,
), an identical
propositional system, 
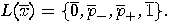
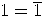 and absurdities
and absurdities
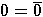 and keep all other propositions intact.
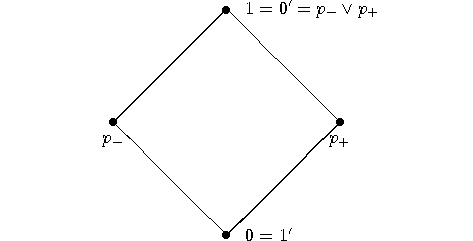
The result is the M0
and keep all other propositions intact.
The result is the M0 propositional structure presented in Figure 11. It is easy to see that M0
propositional structure presented in Figure 11. It is easy to see that M0 is not any longer
a Boolean algebra, since distributivity is not satisfied, as the following
example shows:
is not any longer
a Boolean algebra, since distributivity is not satisfied, as the following
example shows: 
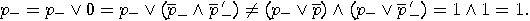
 is an orthocomplemented
lattice, that is, any two elements
have a least upper bound and a greatest lower bound,
is an orthocomplemented
lattice, that is, any two elements
have a least upper bound and a greatest lower bound, 
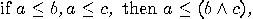
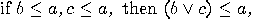
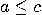 , the modular law is satisfied:
, the modular law is satisfied: 
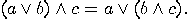

 . _
. _
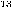 This can
be obtained with a Stern-Gerlach type of experiment.
This can
be obtained with a Stern-Gerlach type of experiment.