|
|
|
|




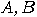 ), and on the other one two
other types (
), and on the other one two
other types (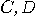 ). The results
are binary, so they will be denoted by “
). The results
are binary, so they will be denoted by “ " and “
" and “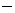 ". We will repeat these
measurements to ensure statistically relevant results. Correlations appear when measurements give the same outcome, that is, “
". We will repeat these
measurements to ensure statistically relevant results. Correlations appear when measurements give the same outcome, that is, “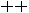 ” and “
” and “ ”.
The basic result is that in almost all cases, more “
”.
The basic result is that in almost all cases, more “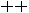 ” and “
” and “ ”
(and less “
”
(and less “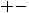 ” and “
” and “ ”) coincidences are recorded than one can explain
by any local classical analysis.
”) coincidences are recorded than one can explain
by any local classical analysis. 
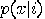 be the probability
that, by taking the measure
be the probability
that, by taking the measure 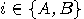 on the first system, the outcome will be
on the first system, the outcome will be 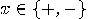 ;
; 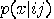 is the probability that by taking the measure
is the probability that by taking the measure
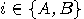 on the first system and the
measure
on the first system and the
measure  on the second,
the outcome of the first system alone
will be
on the second,
the outcome of the first system alone
will be 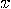 ;
; 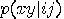 is the probability
that by taking the measure
is the probability
that by taking the measure 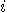 on the first
system and measure
on the first
system and measure 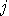 on the
second system, the outcomes will be respectively,
on the
second system, the outcomes will be respectively, 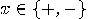 and
and 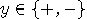 ; finally,
; finally, 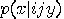 is the probability that when taking the measures
is the probability that when taking the measures 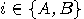 on the first system and
on the first system and  on the second one, and having
outcome
on the second one, and having
outcome 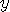 on the second,
the outcome of the first will be
on the second,
the outcome of the first will be 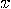 .
. 

If the outcomes of the experiments on both systems
are independent, that is 
 |



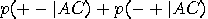
 |
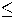  |
  |
  |
  |
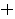  |
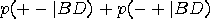  |
  |
  |
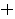  |
  |
(11) |



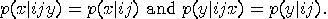




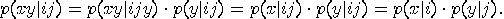

 for
for 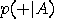 and
and 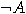 for
for 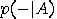 , and similarly for
, and similarly for 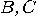 . Further on, let us notice
that the elementary operations with probabilities can be reformulated as
logical operations, namely, conjunction
. Further on, let us notice
that the elementary operations with probabilities can be reformulated as
logical operations, namely, conjunction 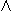 will correspond to product, disjunction
will correspond to product, disjunction 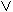 to sum, and implication
to sum, and implication 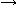 to
to 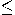 .
. 

If the conjunction is distributive with respect
to disjunction for all propositions 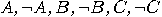 , that is, , that is, 
 |

















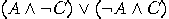  |
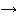  |
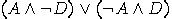  |
  |
  |
  |
  |
  |
  |
  |
  |
  |
  |
  |
  |
  |

 The failure
of independence affects Reichenbach’s [116] causality principle:
two correlated (non independent) events have a common cause, that there exists
an event in their “past" with respect to which they are independent. So,
we arrive at the idea of synchronicity
that has important implication for
quantum computing:
The failure
of independence affects Reichenbach’s [116] causality principle:
two correlated (non independent) events have a common cause, that there exists
an event in their “past" with respect to which they are independent. So,
we arrive at the idea of synchronicity
that has important implication for
quantum computing: 
there exist events which are correlated in a way
which is neither casual nor causal.  |


 Quantum mechanics has chosen to drop separability.
Quantum mechanics has chosen to drop separability.