Noise-driven Concurrent Stereo Matching
  HOME   
 
  Location: NCSM >Introduction
Subsections

Introduction

This chapter outlines the basics of computational stereo including the geometry of stereo systems, discusses the ill-posedness of stereo matching problems, and considers the most popular constraints used to regularise the problem.

Computational stereo vision is an active research domain in computer vision. A large number of important applications such as surveying and mapping, engineering, architecture, autonomous navigation or vision-guided robotics involve quantitative measurements of coordinates of 3D points from a stereopair or multiple images of a 3D scene obtained from different viewpoints [2,3,4]. Stereo vision is used also in geology, forensics, biology (e.g. growth monitoring), biometrics (e.g. 3D facial models), bioengineering and many other application areas.

These 3D measurements are based on stereo matching that pursues the goal of finding points in stereo images depicting the same observed scene points. The corresponding image points are searched for by estimating similarity between image signals (grey values or colours) under admissible geometric and photometric distortions of stereo images. Generally, reconstruction from stereo pairs is an ill-posed inverse optical problem because the same stereo pair can be produced by many different optical surfaces due to homogeneous (uniform or repetitive) textures, partial occlusions and signal distortions. Occlusions result in image areas with no stereo correspondence in another images, and texture homogeneity yields multiple equivalent correspondences.

In principle, an ill-posed vision problem has to be regularised in order to obtain a solution; in the case of computational stereo vision the regularisation has to bring the solution close to human visual perception [5,6]. However, at present, the best strategies for regularising stereo algorithms with respect to all the sources of ill-posedness is still not clear.


Basics of Computational Binocular Stereo

Binocular stereo vision reconstructs a 3D model of an observed scene from a pair of 2D images capturing the scene from different directions. The reconstruction consists of determining 3D coordinates of all binocularly visible scene points using back-projection or triangulation. All the 3D (spatial) points along a ray through the camera's centre of projection to a particular image point are projected to that image point. Triangulation exploits the fact that each location observed by the two cameras produces a unique pair of image points in these cameras. Figure [*] illustrates triangulation geometry. Let O$ _{L}$ and O$ _{R}$ be the centres of projection of two pinhole cameras. Let P$ _{L}$ and P$ _{R}$ denote positions of the two points in the image planes that represent the same point, P. P is the intersection of the back projected rays $ \overrightarrow{\mathbf{O}_{L}\mathbf{P}}$and $ \overrightarrow{\mathbf{O}_{R}\mathbf{P}}$. This triangulation localises each binocularly visible point represented by the two corresponding image points in a stereopair, provided the corresponding image points P$ _{L}$ and P$ _{R}$ associated with the same point P can be determined. However, to establish correct correspondences between two (or more) stereo images is a very difficult task. Computational stereo matching aims to find the correspondences under constraints on expected 3D scenes and assumptions about admissible geometric and photometric deviations of stereo images.

For example, an epipolar geometry in Figure [*] constrains and thus accelerates the search for corresponding image points. Given a point, P$ _{L}$, in the left image, the search area for the corresponding point, P$ _{R}$, in the right image is significantly reduced by the epipolar constraint. Instead of the whole right image, this area is restricted to the intersection of the right image plane with the epipolar plane (O$ _{L}$O$ _{R}$P). The epipolar plane contains the baseline passing through the projection centres, O$ _{L}$ and O$ _{R}$, and intersecting each image plane in a point called the epipole. Each epipole represents the projection centre of another image. If the image plane is parallel to the baseline, the corresponding epipole is located at infinity along that line. Each epipolar plane intersects both images along epipolar lines, and corresponding image points are located along the associated epipolar lines.

Figure: Epipolar geometry of a stereo pair.
\includegraphics{b2_new.eps}

Generally, each pair of corresponding image points has different 2D $ x$- and $ y$-coordinates in the left and right images, $ \textbf{p}_{L} = (x_{L},y_{L})$and $ \textbf{p}_{R} = (x_{R},y_{R})$. In the most common binocular stereo geometry, the associated epipolar lines are image rows with the same $ y$-coordinate, $ y_R = y_L$. This geometry assumes two identical cameras with the same focal length, parallel optical axes and a baseline parallel to the image planes. Given the geometry of a stereo system (the projection centres and relationships between the 3D and 2D image coordinates), all the binocularly visible points with known corresponding image locations $ (\textbf{p}_{L},\textbf{p}_{R})$may be reconstructed by triangulation. Stereo correspondence is typically specified for each location, $ \textbf{p}_{L}$, in the left image as the coordinate differences, called disparities, or parallaxes, of the corresponding point in the right image, $ \textbf{p}_{r}$. Generally, the disparity is a vector $ \mathbf{d}(\mathbf{p}_{L}) = [x_{l} - x_{r},y_{l}- y_{r}]^{\mathsf{T}}$ of $ x$- and $ y$-disparities.

A disparity map, d, contains the disparity vectors for all the left image points having corresponding points in the right image. For the parallel stereo geometry, the $ y$-disparity is always zero, and a disparity map may contain only the scalar $ x$-disparities $ d(\mathbf{p}_{L}) =x_{l}-x_{r}$. Figure [*] illustrates a simple binocular stereo system with parallel optical axes. The baseline of length, $ b$, is perpendicular to the optical axes, coincides with the 3D $ X$-axis and is parallel to the $ x$-axis in the images. The focal lengths of the cameras are equal to $ f$. The world $ Z$-axis coincides with the optical axis of the left camera. In order to reconstruct the world coordinates, $ \mathbf{P}=[X,Y,Z]^\mathsf{T}$, from the disparity map $ d(x_{L},y_{L})$, the camera geometry parameters, the focal length $ f$ and the baseline $ b$, must be exactly known. Then, the 3D coordinates for the corresponding pair $ \mathbf{p}_{L}=[x_{L}, y_{L}]$ and $ \mathbf{p}_{R}=[x_{R}, y_{R}]$ are:

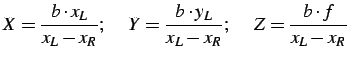$\displaystyle \textbf{$X= \frac{b\cdot x_{L}}{x_{L}-x_{R}}$}; \hspace*{5mm} \t... ..._{L}}{x_{L}-x_{R}}$}; \hspace*{5mm} \textbf{$Z= \frac{b\cdot f}{x_{L}-x_{R}}$}$ (1.1.1)

Figure: Standard geometry of a binocular stereo system.
\includegraphics{b3_new.eps}

According to the configuration in Figure [*], all the observed 3D points can be specified with a vector-valued function, $ \mathbf{S}(X,Y) = [Z(X,Y), I(X,Y)]$, of the planar scene coordinates $ X,Y$. The first component represents the depth value, $ Z$, of the 3D point with planar position, $ (X,Y)$, and the second component represents the optical signal (intensity or colour) attributed to the point $ (X,Y,Z)$. The stereo images are specified with functions $ g_{L}(x_{L},y_{L})$ and $ g_{R}(x_{R},y_{R})$ representing intensities or colours in the image points. Although most typical stereo systems are horizontal, with the left and right cameras displaced along the $ X$-axis, in the general case the baseline can be oriented arbitrarily with respect to the 3D coordinate frame. Thus below, the numerical indices 1 and 2 instead of the letters $ L$ and $ R$ are used to distinguish between the stereo channels.


Stereo Correspondence Problem

Accurate stereo matching to solve the stereo correspondence problem is a key step towards the accurate 3D reconstruction. However, this matching problem is ill-posed and has to be properly regularised to resolve ambiguous solutions [5,6]. The ambiguities have various sources. Even if the scene was a single continuous and visible everywhere surface, matching would remain ambiguous due to image noise caused by cameras and imaging conditions in particular, low signal-to-noise ratio in poorly textured regions, spatially variant and different signal transfer factors in the two stereo channels, and structural ambiguity. Some of these ambiguities could be resolved by using many different views of the same 3D point. This research focuses on only binocular stereo matching and does not consider multiple view stereo problems. In the binocular case, stereo matching is much less capable for reducing structural ambiguity in homogeneous areas yielding many equivalent ``best" correspondences between the images. Here, homogeneity means either uniform (i.e. very small signal deviations) or repetitive of closely similar signal groups. In addition, photometric distortions make each projected intensity, $ I(X,Y)$ of a point, differ in the corresponding points, i.e. $ g_{1}(x_{1},y_{1})$ and $ g_{2}(x_{2},y_{2})$may differ due to mutual spatially variant contrast and offset deviations between the corresponding areas. Simultaneously, these areas have geometrical distortions - due to projective distortions depending on the surface variations $ Z(X,Y)$ - and stereo matching has to take account of these differences.

Also, viewing the same scene by the two mutually displaced cameras results in different visibility conditions: while most of the 3D points are visible to the both cameras - binocularly visible points (BVP) -, some points are occluded by other parts of a scene from one. These monocularly visible points (MVP) appear only in one image of a pair, and therefore have no stereo correspondence at all. A few examples of occlusions are presented in Figure [*]. Two kinds of surface discontinuities in a scene result in large disparity ``jumps", when a thin foreground object appears in front of distant background or conversely a small hole existing at the foreground surface allows us to see the distant background. Detection and accurate recognition of occlusions is very important because incidental correspondences found for such regions may completely compromise the 3D reconstruction.

Figure: Variants of partial occlusions (Red Colour Regions): (a) due to a thin foreground object; (b) due to small foreground hole; (c) due to surface discontinuity.
\includegraphics[width=4.5cm]{b4-1.bmp.eps} \includegraphics[width=4.5cm]{b4-2.bmp.eps} \includegraphics[width=4.7cm]{b4-3.bmp.eps}
(a) (b) (c)

Regularisation of stereo matching involves not only detection of likely occlusions, but also a number of physically justified constraints on observed 3D surfaces and image correspondences. The constraints can reduce false matches and guide the matching process. In particular, the epipolar constraint (see Section [*]) reduces a 2D search space to 1D search along epipolar lines because for any point P$ _{1}$ in one stereo image, the corresponding point P$ _{2}$ lies on the associated epipolar line. The epipolar constraint can be reliably applied only after the geometry of the system is known and a series of corresponding epipolar lines in both stereo images is estimated.

Two other constraints, uniqueness and continuity, first pointed out by Marr and Poggio in 1976 [7] restrict the matching conditions. Uniqueness means that a pixel from one image has only one corresponding pixel in another image. This constraint holds for opaque surfaces, but fails if partially transparent surfaces are present in the scene. The continuity constraint follows from an assumption that a visible surface, and therefore the disparity of corresponding points, varies smoothly almost everywhere over the scene. In the presence of multiple visible surfaces with discontinuities caused by abrupt disparity jumps, this constraint is invalid.

The ordering constraint holds for a single opaque surface and states that the corresponding points along each pair of the associated epipolar lines have the same order. In other words, if a point, $ p_m$, is to the left of the point, $ p_n$, in an epipolar line across one image, then the corresponding point, $ p_{m}^\prime$, is to the left of the point, $ p_{n}^\prime$, respectively, in the associated epipolar line across the second image. This constraint well-known in conventional photogrammetry led to dynamic programming based approaches to stereo matching, by Gimel'farb in 1972 [8] and Baker and Binford in 1981 [9]. The ordering constraint fails for multiple discontinuous surfaces, e.g. for thin foreground objects in front of a distant background ( see e.g. Figure [*],a).

The compatibility constraint [10] used in the majority of known approaches to intensity-based stereo matching states that either the corresponding pixels have closely similar intensity values or the corresponding image windows have high cross-correlation values. The former assumption fails under photometric distortions of stereo images, e.g. under spatially variant or invariant contrast and offset deviations. The latter assumption fails under spatially varying pixel disparities, partial occlusions, and spatially variant contrast and offset deviations.

Thesis Outline

After discussing commonly used stereo matching approaches, this thesis proposes an alternative approach called Noise-driven Concurrent Stereo Matching (NCSM) that overcomes, to some extent, the drawbacks of the more conventional algorithms. Chapter [*] presents an overview of the conventional algorithms and formulates a new NCSM framework based on accurate modelling and estimation of image noise. Chapter [*] considers the main sources of noise in stereo images and discusses in detail the proposed noise-driven NCSM, including different ways of noise estimation, noise-based image segmentation, selection of candidate 3D volumes of admissible stereo matching, and fitting 2D surfaces to the volumes. Chapter [*] presents experimental results obtained for several stereo pairs with known ground truths using NCSM and more conventional stereo matching techniques including the best performing at present graph minimum-cut and belief propagation based algorithms. Finally, Chapter [*] summarises results presented in the thesis and discusses directions of future research.

The work presented in this thesis has been reported in publications [11,12,13,14,15,16,17,18]. One paper [15] received the Second Best Paper Award of the Fourth Mexican International Conference on Artificial Intelligence (MICAI). Monterrey, Mexico Novermber 14-18, 2005, and another [17] received the Best Paper Award of Image and Vision Computing New Zealand (IVCNZ) 2005 conference.

@Copyright by Jiang Liu Contact Administrator jliu001@gmail.com