8 Trespassing the NP Barrier

It is widely believed that quantum computers are more efficient than classical computers. Is quantum computing able to break the NP barrier, i.e., to solve an NP-complete problem in polynomial time? Note that it is not known whether factoring is NP-complete, so Shor’s algorithm cannot be cited (yet?) in this context.

In [
16
] one shows that relative to an oracle chosen uniformly at random, with probability 1, no quantum Turing machine can solve an NP-complete problem in time o Recall that an oracle is a special subroutine whose invocation only costs a unit time. This result does not rule out the possibility that NP
Recall that an oracle is a special subroutine whose invocation only costs a unit time. This result does not rule out the possibility that NP  BQP (the class of problems that can be solved in polynomial time by quantum Turing machines with error probability bounded by 1/3, for all inputs), but shows that there is no black-box approach to solving NP-complete problems in polynomial time on quantum Turing machines.
BQP (the class of problems that can be solved in polynomial time by quantum Turing machines with error probability bounded by 1/3, for all inputs), but shows that there is no black-box approach to solving NP-complete problems in polynomial time on quantum Turing machines.

An interesting hybrid approach has been recently proposed by Ohya and Volovich in [
108
]. We will briefly present their solution which combines quantum and classical machines. As an example we will discuss the satisfiability problem (SAT), the problem to determine whether or not a formula in CNF form is satisfiable.

Let  be a set of Boolean variables. A literal is a variable
be a set of Boolean variables. A literal is a variable  it is complement
it is complement  A Boolean formula is in CNF form if it is a product of disjunctions of literals. For example, the formula
A Boolean formula is in CNF form if it is a product of disjunctions of literals. For example, the formula  is in CNF form. The disjunctions
is in CNF form. The disjunctions  are called clauses. A formula in CNF form is said to be satisfiable _if there is an assignment of 0/1 values to variables such that the formula has value 1. For example. the preceding formula is satisfiable for
are called clauses. A formula in CNF form is said to be satisfiable _if there is an assignment of 0/1 values to variables such that the formula has value 1. For example. the preceding formula is satisfiable for 



For every  where
where  we define the Boolean polynomial
we define the Boolean polynomial


where  is the sum modulo 2. With this notation, SAT is the problem to determine, for every
is the sum modulo 2. With this notation, SAT is the problem to determine, for every  whether there exists a vector
whether there exists a vector  such that
such that 

To exploit quantum parallelism, we will work with the  -tuple tensor product Hilbert space
-tuple tensor product Hilbert space 
 C
C with the computational basis
with the computational basis  where
where  are
are  or
or  We denote
We denote  The quantum version of the function
The quantum version of the function  is given by the unitary operator
is given by the unitary operator  which can be built in polynomial time. Now let us use the usual quantum algorithm:
which can be built in polynomial time. Now let us use the usual quantum algorithm:

Step 1. Produce from the input  the superposition
the superposition


Step 2. Use the unitary matrix  to calculate
to calculate 


Step 3. Measure the last qubit, i.e., apply the projector  to the state
to the state  If we get a click, then the answer is afirmative; otherwise, it is negative. _
If we get a click, then the answer is afirmative; otherwise, it is negative. _

The probability to detect the relation  is
is  , where
, where  is the number of roots of the equation
is the number of roots of the equation  If
If  is suitably large, then the procedure works fine. The tricky situation is when
is suitably large, then the procedure works fine. The tricky situation is when  is very small.
is very small.

Further on, let us notice that after the Step 2 the quantum computer will be in the state


where  and
and  are normalized
are normalized  qubit states and
qubit states and  Consequently, the problem has been reduced to the following problem involving only one qubit: For an arbitrary state
Consequently, the problem has been reduced to the following problem involving only one qubit: For an arbitrary state


distinguish between the cases  and
and  (especially when
(especially when 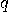 is a very small positive real).
is a very small positive real).

Bennett, Bernstein, Brassard and Vazirani [
16
] argued that a quantum computer can speed-up the solvability of NP-complete problems quadratically but not exponentially: The no-go theorem states that if the inner product of two quantum states is close to 1, then the probability that a measurement distinguishes between them is exponentially small. Is amplification of distinguishability possible?

A possible solution comes from the chaotic behaviour of the classical logistic map which has been discussed in Subsection
3.6
. We start with the above quantum algorithm performing computations with the output  and continue with a classical computation of the logistic map. The connection should be done in such a way that the state
and continue with a classical computation of the logistic map. The connection should be done in such a way that the state  is transformed into the density matrix of the form
is transformed into the density matrix of the form  where
where  and
and  are projectors to the state vectors
are projectors to the state vectors 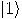 and
and  The density matrix
The density matrix  above is interpreted as the initial data
above is interpreted as the initial data  for the computation of the logistic map as
for the computation of the logistic map as  where
where  is the identity matrix and
is the identity matrix and  is the
is the  -component of Pauli matrix on
-component of Pauli matrix on  A simple computation shows that
A simple computation shows that  and
and  hence the question is whether we can find
hence the question is whether we can find  in polynomial time (in
in polynomial time (in  ) satisfying the inequality
) satisfying the inequality  , for very small but non-zero
, for very small but non-zero 

If  , then
, then  and we obtain
and we obtain  , for all
, for all  If
If  the stochastic dynamics leads to the amplification of the small magnitude
the stochastic dynamics leads to the amplification of the small magnitude  into
into  a process requiring at most
a process requiring at most  steps. The transition from
steps. The transition from  to
to  is nonlinear.
is nonlinear.





 Recall that an oracle is a special subroutine whose invocation only costs a unit time. This result does not rule out the possibility that NP
Recall that an oracle is a special subroutine whose invocation only costs a unit time. This result does not rule out the possibility that NP  BQP (the class of problems that can be solved in polynomial time by quantum Turing machines with error probability bounded by 1/3, for all inputs), but shows that there is no black-box approach to solving NP-complete problems in polynomial time on quantum Turing machines.
BQP (the class of problems that can be solved in polynomial time by quantum Turing machines with error probability bounded by 1/3, for all inputs), but shows that there is no black-box approach to solving NP-complete problems in polynomial time on quantum Turing machines. 

 be a set of Boolean variables. A literal is a variable
be a set of Boolean variables. A literal is a variable  it is complement
it is complement  A Boolean formula is in CNF form if it is a product of disjunctions of literals. For example, the formula
A Boolean formula is in CNF form if it is a product of disjunctions of literals. For example, the formula  is in CNF form. The disjunctions
is in CNF form. The disjunctions  are called clauses. A formula in CNF form is said to be satisfiable _if there is an assignment of 0/1 values to variables such that the formula has value 1. For example. the preceding formula is satisfiable for
are called clauses. A formula in CNF form is said to be satisfiable _if there is an assignment of 0/1 values to variables such that the formula has value 1. For example. the preceding formula is satisfiable for 



 where
where  we define the Boolean polynomial
we define the Boolean polynomial 

 is the sum modulo 2. With this notation, SAT is the problem to determine, for every
is the sum modulo 2. With this notation, SAT is the problem to determine, for every  whether there exists a vector
whether there exists a vector  such that
such that 

 -tuple tensor product Hilbert space
-tuple tensor product Hilbert space 
 C
C with the computational basis
with the computational basis  where
where  are
are  or
or  We denote
We denote  The quantum version of the function
The quantum version of the function  is given by the unitary operator
is given by the unitary operator  which can be built in polynomial time. Now let us use the usual quantum algorithm:
which can be built in polynomial time. Now let us use the usual quantum algorithm: 
 the superposition
the superposition 

 to calculate
to calculate 


 to the state
to the state  If we get a click, then the answer is afirmative; otherwise, it is negative. _
If we get a click, then the answer is afirmative; otherwise, it is negative. _
 is
is  , where
, where  is the number of roots of the equation
is the number of roots of the equation  If
If  is suitably large, then the procedure works fine. The tricky situation is when
is suitably large, then the procedure works fine. The tricky situation is when  is very small.
is very small. 


 and
and  are normalized
are normalized  qubit states and
qubit states and  Consequently, the problem has been reduced to the following problem involving only one qubit: For an arbitrary state
Consequently, the problem has been reduced to the following problem involving only one qubit: For an arbitrary state 

 and
and  (especially when
(especially when 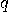 is a very small positive real).
is a very small positive real). 

 and continue with a classical computation of the logistic map. The connection should be done in such a way that the state
and continue with a classical computation of the logistic map. The connection should be done in such a way that the state  is transformed into the density matrix of the form
is transformed into the density matrix of the form  where
where  and
and  are projectors to the state vectors
are projectors to the state vectors 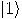 and
and  The density matrix
The density matrix  above is interpreted as the initial data
above is interpreted as the initial data  for the computation of the logistic map as
for the computation of the logistic map as  where
where  is the identity matrix and
is the identity matrix and  is the
is the  -component of Pauli matrix on
-component of Pauli matrix on  A simple computation shows that
A simple computation shows that  and
and  hence the question is whether we can find
hence the question is whether we can find  in polynomial time (in
in polynomial time (in  ) satisfying the inequality
) satisfying the inequality  , for very small but non-zero
, for very small but non-zero 

 , then
, then  and we obtain
and we obtain  , for all
, for all  If
If  the stochastic dynamics leads to the amplification of the small magnitude
the stochastic dynamics leads to the amplification of the small magnitude  into
into  a process requiring at most
a process requiring at most  steps. The transition from
steps. The transition from  to
to  is nonlinear.
is nonlinear. 

