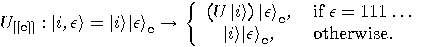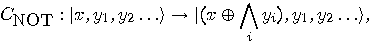5.3 Quantum implementations

Recall that for any function 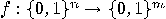 there exists a quantum function
there exists a quantum function  working on an
working on an  -qubits input and an
-qubits input and an  -qubits output register with
-qubits output register with 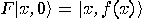 . Invertible functions
. Invertible functions  can be directly realized by quantum functions
can be directly realized by quantum functions 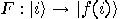 . While a direct implementation of
. While a direct implementation of 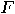 is possible with any universal set of quantum gates, the implementation can be substantially more efficient. For example, if we have efficient implementations of the quantum functions
is possible with any universal set of quantum gates, the implementation can be substantially more efficient. For example, if we have efficient implementations of the quantum functions 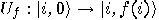 and
and 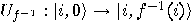 , then an overwriting operator
, then an overwriting operator 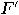 can be constructed by using an
can be constructed by using an  -qubit scratch register:
-qubit scratch register:

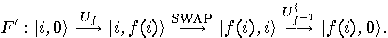
Bennett’s “uncomputing" procedure to control the amount of “junk” bits necessary to compute reversibly non-reversible functions can be presented as follows:

Here 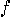 is the composition of two non-reversible functions
is the composition of two non-reversible functions 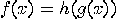 (
( and
and 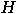 are the quantum functions for
are the quantum functions for 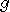 and
and  ). The last step is merely the inversion of the first step and uncomputes the intermediate result. The second register can then be reused for further computations.
). The last step is merely the inversion of the first step and uncomputes the intermediate result. The second register can then be reused for further computations.

If the computation of a function 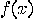 fills a scratch register with the junk bits
fills a scratch register with the junk bits 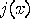 (i.e.
(i.e. 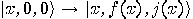 ), a similar procedure can free the register again:
), a similar procedure can free the register again:

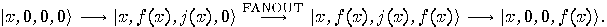
Again, the last step is the inversion of the first. The intermediate step is a 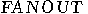 operation which copies the function result into an additional empty register. Possible implementations of
operation which copies the function result into an additional empty register. Possible implementations of 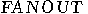 operation are,
operation are,

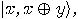
or

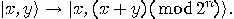
Conditional branching is a powerful tool used by conventional programs. A unitary operator, on the other hand, is static and has no internal flow-control. Nevertheless, we can conditionally apply an  qubit operator
qubit operator 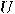 to a quantum register by using an enable qubit and define an
to a quantum register by using an enable qubit and define an 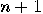 qubit operator
qubit operator 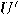


So 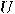 is only applied to basis vectors where the enable bit is set. This can be easily extended to enable-registers of arbitrary length.
is only applied to basis vectors where the enable bit is set. This can be easily extended to enable-registers of arbitrary length.

A conditional operator 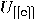 – with enable register
– with enable register  – is a unitary operator of the form
– is a unitary operator of the form

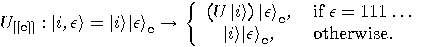
If the architecture allows the efficient implementation of the controlled-NOT gate

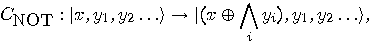
then conditional operators can be realized by simply adding the enable string to the control register of all controlled-not operations.




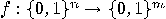 there exists a quantum function
there exists a quantum function  working on an
working on an  -qubits input and an
-qubits input and an  -qubits output register with
-qubits output register with 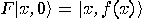 . Invertible functions
. Invertible functions  can be directly realized by quantum functions
can be directly realized by quantum functions 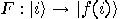 . While a direct implementation of
. While a direct implementation of 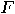 is possible with any universal set of quantum gates, the implementation can be substantially more efficient. For example, if we have efficient implementations of the quantum functions
is possible with any universal set of quantum gates, the implementation can be substantially more efficient. For example, if we have efficient implementations of the quantum functions 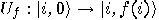 and
and 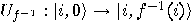 , then an overwriting operator
, then an overwriting operator 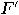 can be constructed by using an
can be constructed by using an  -qubit scratch register:
-qubit scratch register: 

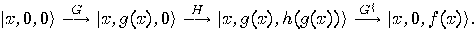
 is the composition of two non-reversible functions
is the composition of two non-reversible functions 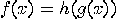 (
( and
and 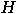 are the quantum functions for
are the quantum functions for 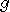 and
and  ). The last step is merely the inversion of the first step and uncomputes the intermediate result. The second register can then be reused for further computations.
). The last step is merely the inversion of the first step and uncomputes the intermediate result. The second register can then be reused for further computations. 
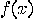 fills a scratch register with the junk bits
fills a scratch register with the junk bits 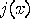 (i.e.
(i.e. 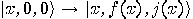 ), a similar procedure can free the register again:
), a similar procedure can free the register again: 
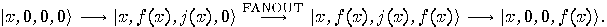
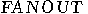 operation which copies the function result into an additional empty register. Possible implementations of
operation which copies the function result into an additional empty register. Possible implementations of 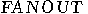 operation are,
operation are, 
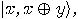

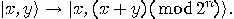
 qubit operator
qubit operator 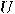 to a quantum register by using an enable qubit and define an
to a quantum register by using an enable qubit and define an 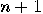 qubit operator
qubit operator 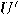


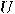 is only applied to basis vectors where the enable bit is set. This can be easily extended to enable-registers of arbitrary length.
is only applied to basis vectors where the enable bit is set. This can be easily extended to enable-registers of arbitrary length. 
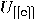 – with enable register
– with enable register  – is a unitary operator of the form
– is a unitary operator of the form