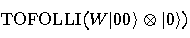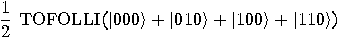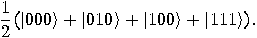5.2 Quantum parallelism

Can the transformation
 , discussed in the above
section, be extended for arbitrary functions
, discussed in the above
section, be extended for arbitrary functions 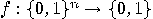 ? Note that to compute a complete set of values
for such a function we need to calculate
? Note that to compute a complete set of values
for such a function we need to calculate 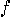 in all
in all  points,
a huge task if
points,
a huge task if  is big (say,
is big (say, 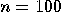 ).
).

The answer is mathematically easy, but computationally extremely powerful,
it points out to one of the most important sources of strength of Quantum
Computing.

Each vector  can be identified
with the state
can be identified
with the state


so keeping in mind that  is a linear transformation, define
is a linear transformation, define  to be the linear operator acting on
to be the linear operator acting on 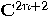 which satisfies the equality (13),
which satisfies the equality (13),

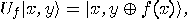
for any 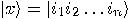 ,
, 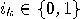 ,
,  and
and 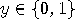 . One can prove that
. One can prove that

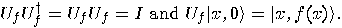
If the transformation  is
applied to an input which is in a superposition then, taking into account
the linearity,
is
applied to an input which is in a superposition then, taking into account
the linearity,  is applied
simultaneously _to all basis
vectors in the superposition and generates a superposition of the results.
Thus it is possible to compute
is applied
simultaneously _to all basis
vectors in the superposition and generates a superposition of the results.
Thus it is possible to compute 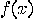 for all the
for all the  values of
values of 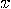 in a single
application of
in a single
application of  . This effect is called quantum parallelism.
. This effect is called quantum parallelism.

Typically, a quantum algorithm starts by preparing the function of interest
in a superposition on all values. Starting with an  -qubit state
-qubit state 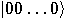 and applying the Walsh–Hdamard transformation
and applying the Walsh–Hdamard transformation
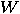 , we get the superposition
, we get the superposition


This superposition is a compact “encoding" of all integers 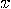 in the interval
in the interval 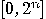 . Using linearity, we get, again, a compact “encoding"
of all values of
. Using linearity, we get, again, a compact “encoding"
of all values of 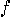 , the function
we are interested in:
, the function
we are interested in:

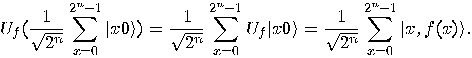
Consequently,  qubits are enough to work
simultaneously with
qubits are enough to work
simultaneously with  states, in a “strange"
compact form; this gives quantum computing the ability to perform an exponential amount of computation in a
linear amount of physical space.
states, in a “strange"
compact form; this gives quantum computing the ability to perform an exponential amount of computation in a
linear amount of physical space.

Let’s apply the above technique to
the simple example of controlled-controlled-NOT gate TOFOLLI that computes
the conjunction.

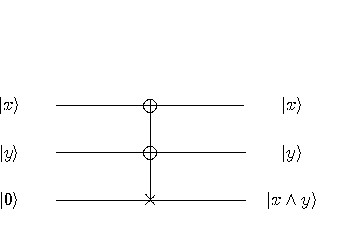

We have:

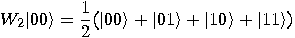
and





The resulting superposition can be viewed as a truth table for conjunction.




 , discussed in the above
section, be extended for arbitrary functions
, discussed in the above
section, be extended for arbitrary functions 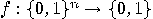 ? Note that to compute a complete set of values
for such a function we need to calculate
? Note that to compute a complete set of values
for such a function we need to calculate 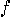 in all
in all  points,
a huge task if
points,
a huge task if  is big (say,
is big (say, 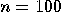 ).
). 

 can be identified
with the state
can be identified
with the state 

 is a linear transformation, define
is a linear transformation, define  to be the linear operator acting on
to be the linear operator acting on 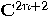 which satisfies the equality (13),
which satisfies the equality (13), 
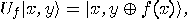
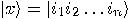 ,
, 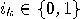 ,
,  and
and 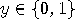 . One can prove that
. One can prove that 
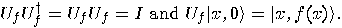
 is
applied to an input which is in a superposition then, taking into account
the linearity,
is
applied to an input which is in a superposition then, taking into account
the linearity,  is applied
simultaneously _to all basis
vectors in the superposition and generates a superposition of the results.
Thus it is possible to compute
is applied
simultaneously _to all basis
vectors in the superposition and generates a superposition of the results.
Thus it is possible to compute 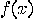 for all the
for all the  values of
values of 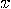 in a single
application of
in a single
application of  . This effect is called quantum parallelism.
. This effect is called quantum parallelism. 
 -qubit state
-qubit state 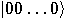 and applying the Walsh–Hdamard transformation
and applying the Walsh–Hdamard transformation
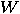 , we get the superposition
, we get the superposition 

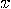 in the interval
in the interval 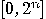 . Using linearity, we get, again, a compact “encoding"
of all values of
. Using linearity, we get, again, a compact “encoding"
of all values of 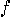 , the function
we are interested in:
, the function
we are interested in: 
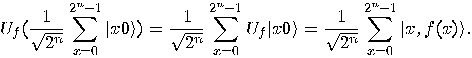
 qubits are enough to work
simultaneously with
qubits are enough to work
simultaneously with  states, in a “strange"
compact form; this gives quantum computing the ability to perform an exponential amount of computation in a
linear amount of physical space.
states, in a “strange"
compact form; this gives quantum computing the ability to perform an exponential amount of computation in a
linear amount of physical space.