Gibbs random field modelling of stochastic textures
Of course, this approach is workable only if a texture is
homogeneous not only to our eye but in some formal way, namely,
if its local statistical features do not depend on translations
within the image. Therefore all the textures can be split into
two groups: stochastic textures that can be efficiently
modelled by multiple pairwise pixel interactions and non-stochastic
ones that do not possess the desired translation invariance.
Several examples of stochastic and non-stochastic textures
will help you to catch the main differences between the both groups.
|
STOCHASTIC vs. NON-STOCHASTIC TEXTURES
|
|---|
| Training sample | Simulated sample
|
| Training sample | Simulated sample
|
|---|
| MIT VisTex Flowers0001 (ST)
|
| MIT VisTex Flowers0002 (ST)
|

|

|
|

|

|
| MIT VisTex Flowers0003 (NST)
|
| MIT VisTex Flowers0004 (ST)
|

|

|
|

|

|
| MIT VisTex Flowers0005 (ST)
|
| MIT VisTex Flowers0006 (ST?)
|

|

|
|

|
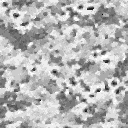
|
| MIT VisTex Flowers0007 (ST)
|
| MIT VisTex Grass0001 (NST)
|

|

|
|

|

|
| MIT VisTex Grass0002 (NST)
|
| MIT VisTex Leaves0010 (NST)
|

|

|
|

|

|
| MIT VisTex Leaves0011 (NST?)
|
| MIT VisTex Metal0000 (ST)
|

|

|
|

|

|
| MIT VisTex Metal0001 (ST)
|
| MIT VisTex Metal0002 (ST)
|

|

|
|

|

|
| MIT VisTex Metal0003 (ST?)
|
| MIT VisTex Metal0004 (ST?)
|

|

|
|

|

|
Some novel results in learning characteristic interaction
structures of pairwise pixel interactions for modelling regular
textures were obtained in 1998 - 2000: first, using an original
empirical iterative learning, by Dr. Alexey
Zalesny (ETHZ, Zurich, Switzerland) who was my PhD student a decade
ago; then I have found that almost similar results can be obtained
analytically, too.
You may look through my recent
papers on that topic (pdf-files) to see which non-stochastic regular
textures can still be efficiently simulated with the
Gibbs models under consideration:































