CONTENTS
Correlation matching
In correlation-based methods, the elements to match are image windows of fixed
size, and the similarity criterion is a measure of the correlation between windows
in the two images. The corresponding element is given by the window that maximises
the similarity criterion (called also similarity measure, or score) within a search region.
Correlation-based stereo matching is based on simplifying assumptions:
- the canonical stereo geometry with parallel optical axes;
- each observed surface patch is (at least, approximately) planar and parallel
to the image planes; and
- relative contrast and offset signal distortions in the presence of
spatially uniform independent Gaussian random noise (or any central-symmetric noise which
probability density function has a monotone inverse dependence of the sum of squared noise values).
Under these assumptions, stereo correspondence has to be established between two
rectangular windows of the same
size S0 = (2a+1)×(2b+1) representing the
desired planar
surface patch in the images of a stereo pair. The correlation relates
closely to the minimum distance D12:x,y
between the corresponding signals in the windows.
Let g1 =
(g1:x,y: x = 0,1,…,M1−1;
y = 0,1,…,n1−1) and
g1 =
(g2:x,y: x = 0,1,…,M2−1;
y = 0,1,…,n2−1) be images of a stereo pair.
Let the same rectangular window with sides being parallel to the image coordinate axes be placed onto
g1 and g2 so that the window
centres coincide with a pixel (x′,y′) in g1 and
a pixel (x,y) in g2:
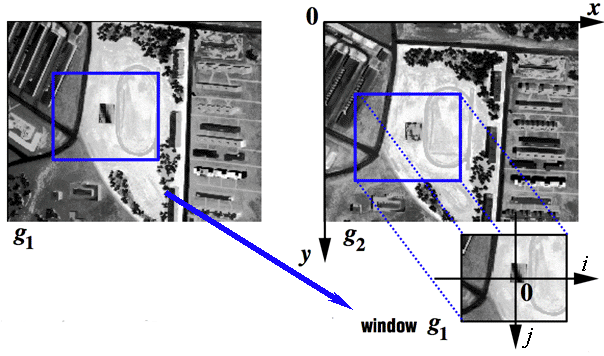
Suppose the window in g1 is fixed whereas the window in g2
can be placed to different candidate positions (x,y) within a search region.
For every such position, the
dissimilarity between the two windows
is computed by minimising the squared distance between the corresponding signals in
the windows with respect to allowable relative distortions, e.g. to
the uniform contrast and offset distortions of the window in g2 comparing
to the fixed window in g1. Indices i and j below denote
relative pixel coordinates relative to the centre of the window;
m1:x′,y′, S11:x′,y′
and m2:x,y,
S22:x,y
are the mean signal value and
the total squared signal deviation over the window in
each image, and S12x′,y′,x,y is the
cross-product of the two centred windows:
The cross-correlation 
is most frequently
used as similarity measure instead of the whole distance-based dissimilarity measure
.
For a window centred in position (x′,y′) in an image
g1 of a stereo pair,
the search for
for the minimum dissimilarity or the maximum correlation exhausts positions (x,y) of the
window centre within
a search region SR
in the other image, g2. Let (x*,y*) be the
optimum position found in g2:
.
Then the disparity vector for the position
(x′,y′) in g1 is
dx′,y′
= [dx′,y′ = x′ − x*,
δx′,y′ =
y′ − y*]T. If the images are
rectified (i.e. have epipolar scan-lines), the y-disparity is always zero, and the
search region for every position (x′,y) in g1
is reduced to a single scanline y in g2:
x′−dmax ≤ x ≤
x′−dmin;
dx′,y = x′ − x*:
Provided that the cameras have parallel optical axes or fixate a common point at a
distance much larger than the baseline, the initial location of the search region in the
right image can
be chosen at the same location as the point in the left image, (x′,y′).
The size of the search region can be estimated from the maximum range of distances
expected in the scene (the disparity is inversely proportional to the distance Z
from the cameras). Moreover, due to the epipolar constraint, the search region
can always be reduced to an 1-D segment along the epipolar line in the right image
which is conjugate to the epipolar line containing the point (x′,y′)
in the left image.
The factor α∗ specifying relative contrast of one window with respect
to the other, and the signal variances S11:x′,y′ and
S22:x,y should
be restricted for excluding inadequate matching results. In particular, if
both the variance S11:x′,y′ and
the cross-product S12:x′,y′,x,y are equal
to zero due to an uniform window in g1 with
constant signals, g1:x+i,y+j = const,
then such a window is similar to any arbitrary window in the other image provided that zero contrast is
allowed. In practice, the contrast between corresponding parts in stereo images
is changing in a relatively narrow range αmin ≤ α ≤ αmax, and
the matching scope has to take this constraint into account:
Return to the local table of contents
Return to the global table of contents
The correlation matching is easily implemented, but its straightforward implementation
is inefficient due to redundant computations in the overlapping windows. For an image
size MN, window size S0, and search region size Δ, the
complexity of straightforward implementation is O(MNS0Δ)
assuming that M1=M2=M and
n1=n2=n.
But it can be reduced to O(MNΔ), i.e. made independent of the window
size, if sums of signals, their products and squares can be stored. For instance, let
an array Ψ = (ψu,v: u = 0,1,…,M−1;
v = 0,1,…,n−1) keep the sums of squared signals
of g1:
Time to fill in the array is O(MN)
due to only three addition / subtraction operations per entry ψ(u,v).
Then the sum U11 of the
squared signals within any window, say, of
the size S0 = (2a+1)×(2b+1)
and centred in the position (x′,y′), is computed also with only
three addition / subtraction operations per window:
Figure below exemplifies the calculation of the window sums:
|
Left - the straighforward sum in the window 5×4:
0+0+1+2+0+0+1+1+0+0+1+2+0+0+2+1+0+0+1+2 = 14
|
Right - the fast sum in the same window using the accumulator:
62−40−23+15 = 14
|
Return to the local table of contents
Return to the global table of contents
The simplest symmetric correlation matching assumes canonical epipolar geometry with
only frontal planar surfaces being parallel to the image plane to in the object space,
independent contrast (α) and offset (β) signal deviations in the images with respect
to an unknown noiseless cyclopean image g of the surface, and additive independent
normal noise in every image with zero mean and the same variance. Provided that the
matching score minimises the maximum of the two squared distances between the image
signals and closely adapted to them signals of the cyclopean image, the dissimilarity
score is derived as follows (here, d is the disparity between the positions of
the windows in both images such that the window cemtres are projected to the position
(x,y) in the object space):
The unconstrained minimisation by β and the constrained minimisation by α
result in the following symmetric matching score:
where
The canonical (epipolar) geometry of stereo images and the
symmetric matching allows us to perform the search in the cyclopean object space
that exhausts positions of a rectangular frontal planar patch in the object space
centred at the cyclopean location (x,y). For each disparity value d,
the patch is represented by two windows in the left
and right images centred at locations (x+d/2,y) and
(x+d/2,y), respectively. The so-called
least-squares correlation extends such matching
to a more general case of slant planar patches. Projective transformations
of the patches are approximately represented by affine parameters, e.g.
x" = α1x′ +
α2y′ +
α3; and
y" = α4x′ +
α5y′ +
α6
that establish correspondence between the left window and the deformed right window.
If the approximate value of these parameters
are known, the linearised signal model (i.e. the Taylor's expansion restricted to
only the linear term) allows for analytical refinement of them. The refinement uses
approximate partial derivatives of the signals in the windows which are smoothed to
suppress the image noise.
Although the least-squares correlation and various attempts to heuristically adapt the window
size to stereo images may improve in some cases the matching results,
generally the correlation-based stereo has serious shortcomings because it cannot
appropriately account for realistic geometric differences between the images. The conjugate
images of a stereo pair are perspective projections of the 3-D scene, and surface slope,
discontinuities, and different positions and orientations
of the cameras result in geometric distortions that influence image correspondence.
The assumed frontal planes are too imprecise approximations of natural surfaces.
Also, the correlation does not work well if the windows to be matched are either
almost uniform (a dominant low frequency content) or too textured (a dominant high
frequency content). Moreover, it is not obvious how to choose an adequate window size
and shape in each position because they depend on the unknown observed optical surface.
Return to the local table of contents
Return to the global table of contents